

Next: Foliaciones y lineaciones
Up: estruct
Previous: Fallas
Subsecciones
Usaremos el término dúctil para referirnos a una deformación
permanente, en estado sólido, en la cual no hay pérdida de
cohesión a escala de granos cristalinos o mayores.
Esta definición excluye flujos cataclásticos de la transición
frágil-dúctil.
Veremos en primer lugar las estructuras que se forman en las rocas
como resultado de esta deformación.
Son las estructuras más obvias y comunes que reflejan un evento de
deformación dúctil en la corteza. Los pliegues son ondulaciones
tipo onda que se desarrollan durante la deformación. Pueden
ocurrir a cualquier escala y en cualquier tipo de roca.
La gran variedad de formas de pliegues en las rocas reflejan las
condiciones físicas (stress, temperatura y presión) y las
propiedades mecánicas de las rocas al deformarse.
- Elementos descriptivos reales:
- Flancos o limbos: son las zonas menos curvadas conectadas
por la zona de mayor curvatura.
- Charnela: zona de mayor curvatura (menor diámetro de
curvatura).
- Cresta: zona topográficamente más elevada de un
pliegue.
Figura 4.1:
Elementos descriptivos reales.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
- Elementos geométricos:
- Perfil: corte perpendicular a la charnela.
- Eje: línea de orientación específica, ubicada donde la
curvatura es máxima. Describe totalmente la geometría de un
pliegue cilíndrico y en pliegues cónicos es la línea de
referencia.
- Pliegue cilíndrico: tipo de pliegue en el cual una línea de
orientación constante (eje del pliegue) puede ser movida a lo
largo de la superficie plegada sin perder contacto con ella. Los
pliegues que no cumplen con esta condición se denominan pliegues
no cilíndricos.
- Pliegue cónico: pliegue cuya superficie forma un ángulo
distinto a 00 con una línea de orientación fija.
- Superficie axial: superficie que contiene las
charnelas de todas las capas que conforman el pliegue. Puede ser
plana o curva.
Figura 4.2:
Elementos geométricos.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{35mm}{\bf\hfill(Figura)}}}\end{figure}](img29.gif) |
La orientación de los pliegues puede ser expresada a través del
rumbo y buzamiento de la charnela o eje de pliegue y el rumbo y
manteo de la superficie axial.
- Homoclinal
- : no tiene charnela.
- Monoclinal
- : dos limbos largos, horizontales, conectados por
un limbo corto, inclinado.
- Terraza estructural
- : dos limbos largos, inclinados,
conectados por un limbo corto, horizontal.
- Pliegue volcado
- : pliegue recumbente, en el cual un limbo ha
rotado más de 900 desde su posición original.
Figura 4.3:
Términos respecto a la orientación de los pliegues.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{8cm}{\bf\hfill(Figura)}}}\end{figure}](img1.gif) |
(Útiles para describir pliegues)
- Cilindricidad
- Simetría
- Estilo de la superficie plegada
- Estilo de la capa plegada
- Estilo de las multicapas plegadas
Se definirá primero dos ángulos que permiten describir la
intensidad del plegamiento:
- Ángulo de plegamiento,
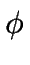 : ángulo entre las normales a
las superficies plegadas en el punto de inflexión.
: ángulo entre las normales a
las superficies plegadas en el punto de inflexión.
- Ángulo interlimbos, i: ángulo que forman las dos tangentes a las
superficies plegadas en el punto de inflexión. Por geometría,
i = 180
0 -
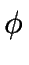
- Mediana: superficie que pasa por los puntos de inflexión.
Figura 4.4:
Ángulos que permiten describir la intensidad del plegamiento.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{60mm}{\bf\hfill(Figura)}}}\end{figure}](img32.gif) |
- Cilindricidad: es el grado en que un pliegue aproxima
su geometría a un pliegue cilíndrico. Es un rasgo que caracteriza
diferentes estilos de plegamiento. La cilindricidad se ve
cuantitativamente en una red equiareal por la distribución de los
polos de la superficie plegada. Un pliegue cilíndrico tiene sus
polos distribuidos en un círculo mayor.
- Simetría: una superficie plegada forma un pliegue
simétrico si, en un perfil, la forma a ambos lados de la charnela
es la misma y también el largo. En los pliegues asimétricos, el
grado de asimetría está determinado por el ángulo de inclinación
entre el bisector del ángulo de plegamiento,
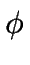 , y la mediana.
El sentido de asimetría depende de la posición en que miremos el
pliegue, por convención definiremos el sentido de asimetría
mirando en dirección del buzamiento del eje del pliegue. Según el
sentido de asimetría los pliegues pueden ser Z o S.
, y la mediana.
El sentido de asimetría depende de la posición en que miremos el
pliegue, por convención definiremos el sentido de asimetría
mirando en dirección del buzamiento del eje del pliegue. Según el
sentido de asimetría los pliegues pueden ser Z o S.
- Pliegue Z: si el limbo más corto ha rotado en sentido
horario con respecto al limbo largo.
- Pliegue S: si el limbo más corto ha rotado en sentido
antihorario con respecto al limbo más largo.
- Estilo de la superficie plegada: la geometría de una
superficie plegada se describe especificando tres elementos:
- Razón del aspecto
- Cierre
- Aspereza
Para definir estas características se requiere construir un
cuadrilátero alrededor del pliegue de modo que los lados sean
tangentes a los limbos en el punto de inflexión y que la parte
superior sea tangente al pliegue y normal al bisector del ángulo
de plegamiento 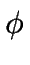 .
.
- Razón del aspecto:
P = A/M
donde A: amplitud del pliegue medido en la superficie axial = alto
del cuadrilátero, M: ancho de la base del cuadrilátero. Si, por
ejemplo, P > 0.1 y P < 0.25, el pliegue es descrito como ancho.
- Cierre (estrechez): definido por el ángulo
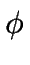 .
.
- Aspereza, b: mide la curvatura relativa del pliegue en la
charnela.
Figura 4.5:
Clasificación de pliegues según la orientación del plano axial y
del eje.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{.85\textheight}{\bf\hfill(Figura)}}}\end{figure}](img34.gif) |
Tabla 4.1:
Razón del aspecto P.
| Término descriptivo |
Razón del aspecto P |
|
| |
P = A/M |
| Ancho |
0, 1  P < 0, 25 P < 0, 25 |
-1  logP < - 0, 6 logP < - 0, 6 |
| Amplio |
0, 25  P < 0, 63 P < 0, 63 |
-0, 6  logP < - 0, 2 logP < - 0, 2 |
| ``Equant" |
0, 5  P P  2 2 |
-0, 2  logP < 0, 2 logP < 0, 2 |
| Corto |
1, 58  P < 4 P < 4 |
0, 2  logP < 0, 6 logP < 0, 6 |
| Alto |
4  P < 10 P < 10 |
0, 6  logP < 1 logP < 1 |
|
Tabla 4.2:
Estrechez (cierre) de pliegues (modificado después de Fleuty(1964)).
| Término descriptivo |
|
Ángulo plegamiento |
Ángulo interlimbos |
| |
|
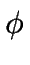 [grados] [grados] |
| Agudo |
Suave |
0 < 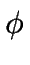 < 60 < 60 |
180 > i > 120 |
| |
Abierto |
60  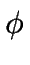 < 110 < 110 |
| |
Cerrado |
110  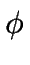 < 150 < 150 |
| |
Estrecho |
150  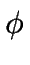 < 180 < 180 |
| Isoclinal |
|
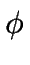 = 180 = 180 |
i = 0 |
| Obtuso |
``Fan" |
180 < 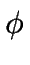 < 250 < 250 |
0 > i > - 70 |
| |
Involuto |
250  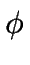 < 360 < 360 |
|
Tabla 4.3:
Aspereza de pliegues.
| Término descriptivo |
Aspereza b |
| Puntiagudo |
0  b < 0, 1 b < 0, 1 |
| Angular |
0, 1  b < 0, 2 b < 0, 2 |
| Subangular |
0, 2  b < 0, 4 b < 0, 4 |
| Subredondeado |
0, 4  b < 0, 8 b < 0, 8 |
| Redondeado |
0, 8  b b  1 1 |
| Áspero |
1 < b  2 2 |
|
- Estilo de la capa plegada: clasificación de Ramsay.
El estilo de la capa plegada se determina comparando el estilo de
las dos superficies de la capa. Se usan tres parámetros
geométricos relativos a un par de líneas paralelas, tangentes a
las superficies de la capa en perfil. Los tres parámetros
geométricos son:
- Isógonas de manteo: línea que une puntos de igual manteo en
superficies opuestas.
- Espesor ortogonal,
t
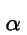 : distancia perpendicular
entre dos tangentes paralelas.
: distancia perpendicular
entre dos tangentes paralelas.
- Espesor de la traza axial,
T
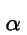 : distancia entre dos
tangentes medida paralelamente a la traza de la superficie axial.
: distancia entre dos
tangentes medida paralelamente a la traza de la superficie axial.
Figura 4.6:
Parámetros geométricos de la clasificación de Ramsay.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{8cm}{\bf\hfill(Figura)}}}\end{figure}](img1.gif) |
Según cómo varían estos parámetros desde la charnela hacia los
limbos (o a mayores valores de 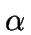 ), se definen diferentes
clases. La inclinación de la superficie plegada en el punto de
tangencia,
), se definen diferentes
clases. La inclinación de la superficie plegada en el punto de
tangencia, 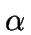 , es el ángulo entre la línea tangente y la
línea normal a la traza de la superficie axial.
, es el ángulo entre la línea tangente y la
línea normal a la traza de la superficie axial.
- Curvatura relativa o variación de las isógonas:
- Si las isógonas convergen hacia el interior del pliegue, la
curvatura de la superficie interna será mayor que la curvatura de
la superficie externa y se definen los pliegues clase 1.
- Isógonas paralelas que son también paralelas a la traza de
la superficie axial definen la clase 2. Los Pliegues de esta
clase de denominan también pliegues similares, porque las
curvaturas de ambas superficies son similares.
- Isógonas que divergen del centro definen la clase 3 e
indican que la curvatura de la superficie externa es mayor.
- Variación en el espesor ortogonal:
- La variación en
t
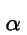 es característica de los
diferentes tipos de pliegues y es la base para subdividir la clase
1.
es característica de los
diferentes tipos de pliegues y es la base para subdividir la clase
1.
- Si
t
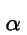 crece desde la charnela hacia los limbos,
los pliegues son de clase 1A.
crece desde la charnela hacia los limbos,
los pliegues son de clase 1A.
- Si
t
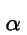 es constante, los pliegues son clase
1B y se denominan pliegues paralelos. (Pliegue concéntrico:
pliegue paralelo cuyas superficies interna y externa tienen
aspereza
b = 1
es constante, los pliegues son clase
1B y se denominan pliegues paralelos. (Pliegue concéntrico:
pliegue paralelo cuyas superficies interna y externa tienen
aspereza
b = 1 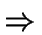 rc = r0).
rc = r0).
- Si
t
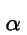 disminuye, la subclase es clase 1C.
disminuye, la subclase es clase 1C.
-
t
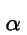 disminuye también para los pliegues clase 2 y
clase 3.
disminuye también para los pliegues clase 2 y
clase 3.
- Variación en el espesor de la traza axial T:
-
T
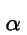 aumenta en la clase 1.
aumenta en la clase 1.
-
T
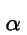 es constante en la clase 2.
es constante en la clase 2.
-
T
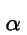 disminuye en la clase 3.
disminuye en la clase 3.
Figura 4.7:
Clases de pliegues de la clasificación de Ramsay.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{9cm}{\bf\hfill(Figura)}}}\end{figure}](img39.gif) |
Tabla 4.4:
Estilo de una capa plegada: clasificación de Ramsay (1967).
| Clase |
Isógonas Manteo |
Espesor Ortogonal |
Espesor Traza Axial |
| |
(desde superficie |
(desde charnela |
(desde charnela |
| |
cóncava a convexa) |
hacia limbos) |
hacia limbos) |
| 1 |
Convergen |
|
Aumentan |
| 1A |
Convergen |
Aumentan |
Aumentan |
| 1B |
Convergen |
Constantes |
Aumentan |
| 1C |
Convergen |
Disminuyen |
Aumentan |
| 2 |
Paralelas |
Disminuyen |
Constantes |
| 3 |
Divergen |
Disminuyen |
Disminuyen |
|
- Estilo de multicapas plegadas.
Un pliegue multicapas está compuesto por varias capas plegadas al mismo
tiempo. El estilo puede ser definido en términos de la armonía
del plegamiento y de la geometría de la superficie axial.
- Armonía del plegamiento.
- En un perfil, todos los pliegues
multicapas terminan en ambas direcciones a lo largo del plano
axial, a menos que la secuencia incluya una superficie libre como
la superficie de la tierra. La profundidad del plegamiento D es
la distancia, a lo largo de la traza de la superficie axial, donde
el plegamiento existe. La armonía H es una medida, independiente
de la escala, de la persistencia o continuidad del plegamiento y
es igual a la razón
D/(
 /2), donde
/2), donde  /2 es la mitad
de una longitud de onda.
/2 es la mitad
de una longitud de onda.
H =
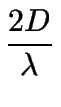
.
Figura 4.8:
Armonía en multicapas plegadas.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{6cm}{\bf\hfill(Figura)}}}\end{figure}](img42.gif) |
Los pliegues se desarrollan simultáneamente a diferentes escalas,
de manera que grandes pliegues incluyen pliegues más pequeños en
sus limbos y en sus zonas de charnela. Los más grandes son
pliegues de primer orden y son generalmente rasgos de escala
regional. Se asigna un número de orden mayor a medida que va
disminuyendo su tamaño. Los pliegues de mayor orden se denominan
también pliegues parásitos.
- Pliegues paralelos
- : estrictamente definidos como clase 1B,
tanto para una capa, como para multicapas. Se extiende su uso a
pliegues de clase 1A y 1C cercanos a 1B.
- Pliegues similares
- : estrictamente tienen geometría clase 2
para una o más capas. Puede extenderse su uso a clase 1C y clase
3.
Figura 4.9:
Pliegues paralelos y similares.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{9cm}{\bf\hfill(Figura)}}}\end{figure}](img39.gif) |
- Pliegues chevrón y kink
- : son pliegues cilíndricos,
armónicos, multicapas clase 2 que tienen charnelas puntiagudas y
limbos cerrados a suaves. Los pliegues chevrón son simétricos y
los kink son asimétricos.
Figura 4.10:
Pliegues chevrón y kink.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
Los pliegues de clase 1B son comunes en muchas áreas deformadas.
La geometría de esa clase de pliegue puede ser explicada como el
resultado de los siguientes mecanismos de plegamiento:
- Flexura ortogonal
- Cizalle flexural
- Flexura por pérdida de volumen
Colectivamente estos tres modelos se denominan plegamiento
flexural. En todos estos modelos, el espesor ortogonal de la capa
se mantiene constante durante el plegamiento (definición de
pliegues de clase 1B) y por lo tanto la clase del pliegue no es
resultado de un mecanismo único.
El plegamiento flexural resulta de flexión (bending) o doblamiento (buckling), que son dos maneras de aplicar fuerzas a
una capa.
- Flexión
- de una capa resulta de la aplicación de pares de
fuerzas que producen torques iguales y opuestos que doblan la capa
formando un pliegue. En flexión pura no hay ni compresión ni
tracción en ninguna dirección. En la figura están mostrados tres
sistemas de fuerzas aplicadas para producir torque (ej. lacolito,
falla en basamento).
- Doblamiento
- (buckling) resulta de la aplicación de stresses
compresivos, paralelos a la capa. Si el stress compresivo es
suficientemente grande, la capa se vuelve inestable y se dobla
formando un pliegue, ya sea por stresses solos o asociados a
torques.
Figura 4.11:
Flexión y doblamiento.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
Es una de las maneras que tiene una capa para responder a fuerzas
de flexión o doblamiento. En este proceso cinemático, todas las
líneas que fueron perpendiculares a la capa antes del plegamiento,
permanecen perpendiculares después del plegamiento. En un corte
perpendicular a la charnela, la superficie de la capa en el lado
convexo del pliegue es estirada y la superficie en el lado cóncavo
es acortada. La superficie que no cambia de largo durante la
deformación se denomina superficie neutral. El espesor
ortogonal se mantiene constante en todo el pliegue.
La flexura ortogonal es característica de pliegues de baja
curvatura desarrollados en capas competentes que son resistentes a
deformación dúctil. A medida que la curvatura aumenta, la
ortogonalidad se va perdiendo.
Figura 4.12:
Flexura ortogonal.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
En este caso, la capa responde a fuerzas de flexión o doblamiento
mediante una deformación de cizalle simple paralela a la capa. En
este caso no hay ni estiramiento ni acortamiento en ninguna
superficie de la capa que forma el pliegue.
El plegamiento por cizalle flexural es análogo al doblamiento de
un conjunto de cartas o tarjetas en el cual todo el movimiento es
paralelo a los planos de cizalle (representado por las
tarjetas). El material del lado convexo de un plano de cizalle se
desplaza hacia la charnela en relación al material del lado
cóncavo. El espesor de la capa, medido perpendicular a los planos
de cizalle es constante. Sin embargo, las líneas que eran
ortogonales antes del plegamiento no lo son después, excepto en la
charnela, ya que la magnitud del cizalle disminuye desde los
flancos hacia la charnela. No hay cambio de largo de ninguna
superficie de la capa.
El plegamiento de cizalle flexural puede ocurrir en vez de flexura
ortogonal si la capa es menos competente y por lo tanto tiene una
fuerte anisotropía planar.
Figura 4.13:
Flujo o cizalle flexural.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
En este mecanismo, un pliegue se forma o es amplificado por una
remoción gradual de material desde zonas particulares de la capa
plegada. La pérdida en general, resulta de disolución. El
mecanismo de pérdida de volumen no resulta en una clase única de
pliegues, porque la geometría del pliegue depende de la
orientación de las zonas de disolución. Los pliegues que se pueden
formar son clase 1B, 1C o 2.
Figura 4.14:
Plegamiento de una capa por pérdida de volumen.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
En este tipo de plegamiento, que se denomina también plegamiento
de flujo pasivo o simplemente plegamiento pasivo, la capa es
altamente incompetente y no ejerce influencia en el proceso de
plegamiento. Ella solamente actúa como un marcador que registra la
deformación. La deformación ocurre por cizalle simple,
inhomogéneo, en planos de cizalle que cortan la capa. El sentido y
cantidad de cizalle varía sistemáticamente para producir el
plegamiento. Este proceso da como resultado pliegues similares o
clase 2.
Para ilustrar la cinemática de este proceso de plegamiento, de
nuevo podemos usar un conjunto de cartas. En este caso, los planos
de cizalle representados por las cartas no son paralelos a la capa
que será plegada, sino que la cortan.
Figura 4.15:
Plegamiento de cizalle pasivo.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif) |
Las propiedades mecánicas de las rocas involucradas en el
plegamiento tienen un efecto importante en el estilo de pliegues
que se desarrollan. Cualitativamento se describe la tasa a la cual
un material dúctil es capaz de deformarse a un stress diferencial
particular en términos de su competencia. Bajo un mismo stress
diferencial un material competente se deforma de manera dúctil a
una tasa relativamente baja comparada con un material
incompetente. Si dos materiales son deformados a igual tasa, el
stress diferencial, para igual deformación, es mayor en el
material competente. Es decir, un material incompetente se deforma
más fácilmente que uno incompetente.
Muchos plegamientos involucran secuencias multicapas que
desarrollan una geometría más compleja que la recién vista. Una de
las causas de esta mayor complejidad es la diferencia en las
propiedades mecánicas que pueden existir entre rocas adyacentes.
Para analizar el plegamiento multicapas se considera la
competencia media de toda la secuencia y el contraste en
competencia entre capas individuales. Se considera primero un
modelo de plegamiento simple que involucre muchas capas de una
competencia alta, pero similar para todas. Luego, se considerará
el efecto de alternar delgadas capas incompetentes con capas
gruesas competentes (alto contraste y competencia media alta).
Finalmente, se considerará el efecto de aumentar la razón entre
material incompetente y material competente en la multicapa
(disminución de la competencia media y alto contraste de
competencia).
Si el contraste de competencia es 0, la multicapa se comporta
como una capa única y de acuerdo a los modelos ya vistos. Incluso
capas de diferente competencia pueden comportarse como capa única.
En este caso, si se desarrolla una superficie neutra, las capas
del lado convexo serán estiradas y adelgazadas en la charnela,
dando como resultado pliegues con geometría clase 1A.
Un conjunto de capas, que tienen escencialmente la misma alta
competencia (alta competencia media) y baja fricción en los planos
de contacto, puede responder a fuerzas de flexión o doblamiento
por un plegamiento de deslizamiento flexural (flexural slip),
donde las capas deslizan libremente. Se originan pliegues clase
1B.
El deslizamiento de una capa sobre otra, conduce comúnmente al
desarrollo de estrías o fibras minerales en los planos de
estratificación perpendiculares al eje del pliegue. En general se
desarrollan en los limbos (donde el deslizamiento es máximo) y no
en la zona de charnela.
Muchos pliegues consisten en un conjunto de capas de espesores
similares, pero de distinta competencia (competencia media moderada, alto
contraste de competencia). En este caso, las capas competentes
como grupo se deforman por flexural slip y el deslizamiento entre
las capas es absorbido por la deformación en las capas
incompetentes. Se desarrolla un pliegue clase 1C.
Si las capas incompetentes son mucho más gruesas que las
competentes (baja competencia media, alto contraste), las capas
incompetentes dominan la deformación a gran escala. El
espaciamiento entre dos capas competentes es tan grande que el
plegamiento flexural de una capa competente no afecta la próxima
y se desarrollan pliegues disarmónicos ptigmáticos. A pesar que
los pliegues de mayor orden en las capas individuales competentes
son clase 1B y 1C, la geometría de los pliegues de menor orden son
cercanos a clase 2 y es dominado por el flujo dúctil de las capas
incompetentes.
Si todas las capas son incompetentes, con bajo contraste (baja
competencia media, bajo contraste) y si las capas no se deslizan
en las interfases, entonces la multicapa es homogénea y las capas
actúan como marcadores pasivos de la deformación, formando
pliegues clase 2.
Figura 4.16:
Cizalle flexural y pasivo de multicapas.
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{.90\textheight}{\bf\hfill(Figura)}}}\end{figure}](img22.gif) |


Next: Foliaciones y lineaciones
Up: estruct
Previous: Fallas
Eduardo Moreno
2001-06-04
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}](img12.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{35mm}{\bf\hfill(Figura)}}}\end{figure}](img29.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{8cm}{\bf\hfill(Figura)}}}\end{figure}](img1.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{60mm}{\bf\hfill(Figura)}}}\end{figure}](img32.gif)
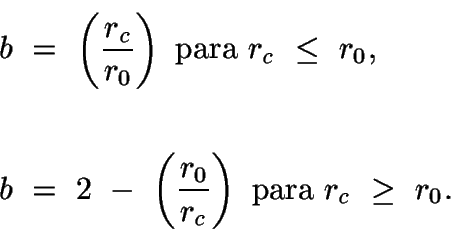
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{.85\textheight}{\bf\hfill(Figura)}}}\end{figure}](img34.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{9cm}{\bf\hfill(Figura)}}}\end{figure}](img39.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{6cm}{\bf\hfill(Figura)}}}\end{figure}](img42.gif)
![\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{.90\textheight}{\bf\hfill(Figura)}}}\end{figure}](img22.gif)