Bote Triple
Una primera pregunta que aparece al ver el diagrama de bifurcaciones con estas raras soluciones asintóticas (bote triple, copias verticales del diagrama, etc.) es si son muy o poco dependientes a las condiciones iniciales. Para responder cuantitativamente a esta pregunta, se usa el concepto de probabilidades y simulaciones con las siguientes caracteríticas:
- La partícula rebota 5000 veces contra la base antes de analizar el tipo de movimiento que tiene. Esta es la fase de relajación del sistema en que se espera que o bien se haya llegado a un movimiento periódico, o bien el régimen sea caótico.
- Para cada coef. y frecuencia revisados, se dan 100.000 condiciones iniciales elegidas al azar. Las rapideces van de 0 a 20 y el la fase del movimiento del piso va de 0 a 2 pi. La altura de la partícula es levemente mayor a la de la base en el tiempo t = 0
- La probabilidad de hallar el bote triple será el cuociente entre las veces en que la partícula llegó a este tipo de movimiento en la familia vertical principal, y el total de casos.
- Primero fijamos el coeficiente de restitución r = 0.8 para distintas frecuencias cercanas a w = 1, el programa se puede descargar aquí
- Segundo, se fija la frecuencia en 1 y se calcula la probabilidad para distintos coeficientes de restitución, el código se puede bajar o ver desde aquí
Resultados:
1) - Usando el coeficiente r = 0.8, barrimos las frecuencias entre w = 0.98 y w = 1.0096, la variación de frecuencias es dw = 0.0001, se puede descargar el archivo de datos generado.
La idea era ver con precisión un inervalo pequeño de frecuencias. La imagen de abajo muestra en la vertical las probabilidades y en la horizontal las frecuencias.

2) - Usando el coeficiente r = 0.8, barrimos las frecuencias entre w = 0.965 y w = 1.09, la variación de frecuencias es dw = 0.001 (10 veces el paso anterior), se puede descargar el archivo de datos generado. Y se adjunta una imagen similar a la anterior.
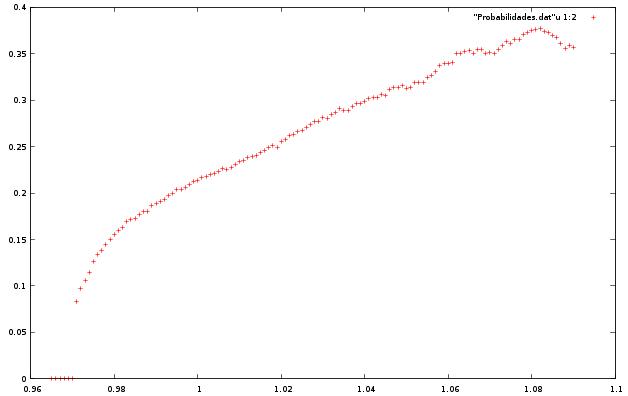
3) - Usando la frecuencia w = 1.0 se barren los coeficientes de restitución entre r = 0.753 y r = 0.905, la variación de restituciones es dr = 0.001, se puede descargar el archivo de datos generado. El siguiente gráfico tiene en la vertical las probabilidades y en la horizontal los valores de los coefs. de restitución.
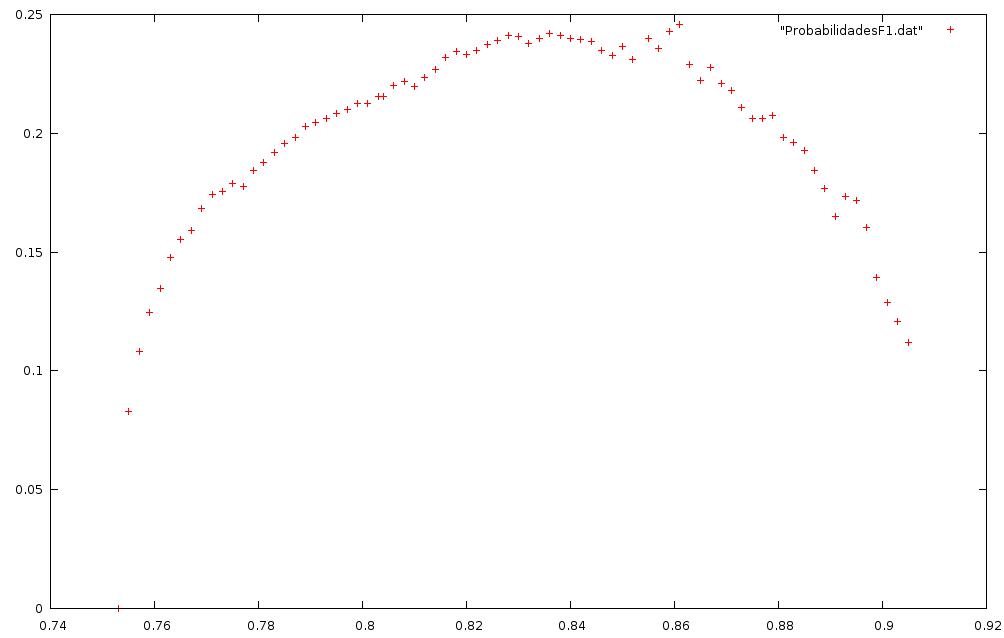
Nótese el aspecto aparentemente simétrico en torno al máximo .