Este programa es una simplificación del que aparece en Analisis y tiene 2000 colisiones iniciales, después de las cuales guarda en un archivo de datos dos columnas: la primera tiene la frecuencia y la segunda tiene las rapideces post-choque.

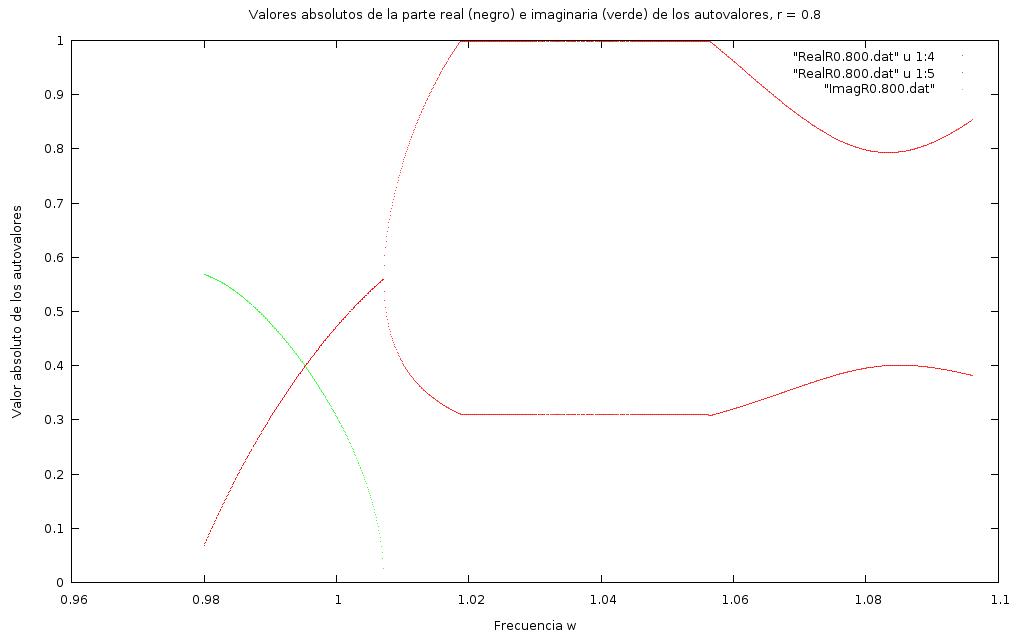
Un ejemplo del tipo de gráficos generados con el programa es la siguiente imagen, en que la restitución es r = 0.8

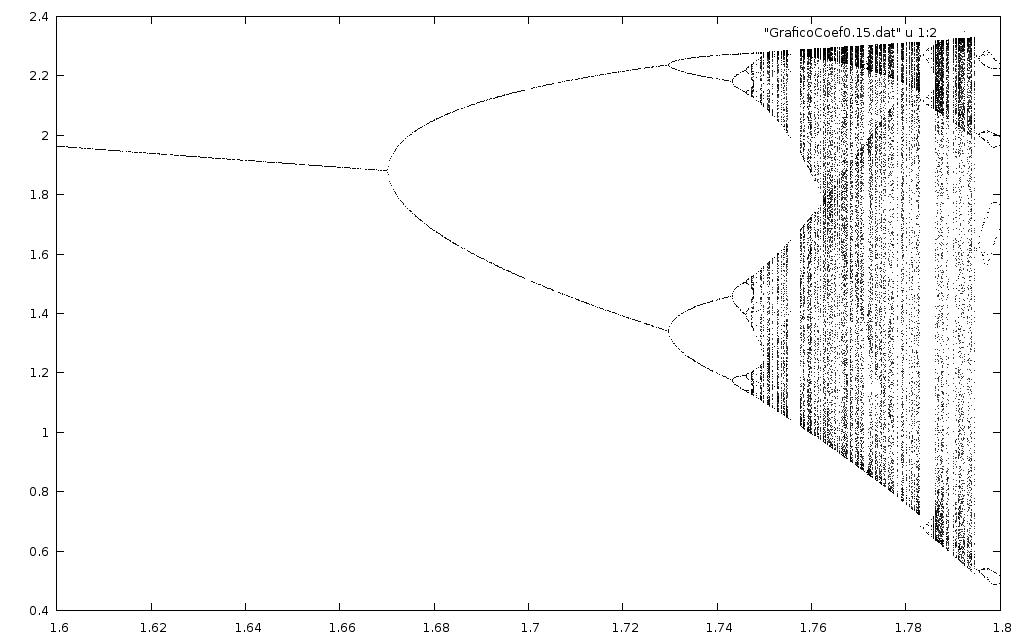
El eje horizontal es de frecuencias de la base y el vertical de velocidades de despegue. La imagen puede ser vista o descargada a una mejor resolución, el archivo que la generó también se puede bajar

El nombre del archivo de datos indica el coeficiente de restitución usado, por ejemplo el archivo GraficoCoef0.80.dat tiene un coeficiente r = 0.8

Es interesante notar que cuando graficamos otras variables como la energía, tiempo de vuelo, altura, etc., en función de la frecuencia con una restitución fija (o bien en función de las restituciones a una fre cuencia fija) se ve el mismo tipo de diagrama.

Se puede descargar un programa que crea un archivo de datos con las posiciones del la partícula y base para distintos tiempos comprendidos entre la colisión 1 y 10 contadas desde la relajación (de 5000 botes para las ejecuciones actuales).

El programa busca el bote triple a lo más 100 veces para cada par de datos coeficiente de restitución y frecuencia.

La siguiente imagen es un ejemplo de lo que resulta al graficar los datos que entrega el programa, en el eje horizontal está el tiempo y en el vertical las alturas. Lo verde es la base y lo rojo es la partícula. Esta trayectoria es de interés porque se hace a una frecuencia w = 0.97081699, que es donde (aproximadamente) aparece el bote triple cuando r = 0.8

Este programa fue usado para hallar la aparición del bote triple

Los puntos fijos de una función de varias variables serán estables sí y sólo sí los módulos de la parte real de los autovalores del jacobiano de la función son estructamente menores que uno. Es importante saber cómo son los autovalores para la función que nos lleva de un punto fijo al siguiente en el bote triple para saber si el término del bote triple es mediante la llamada flip bifurcation (mecanismo con que el diagrama de bifurcaciones para coeficientes bajos, por ejemplo r = 0.15, desdobla las rapideces).

La siguiente imagen es fue obtenido con un programa descargable y en la horizontal están las frecuencias mientras en la vertical hay: en negro los módulos de la parte real de los autovalores, en verde el valor absoluto de la parte imaginaria.

El gráfico se obtuvo al escribir en gnuplot: p "RealR0.800.dat" u 1:4 w d 1, "RealR0.800.dat" u 1:5 w d 1, "ImagR0.800.dat" w d 2

Como se puede ver, los autovalores no alcanzan valores cercanos a la unidad cuando el bote triple desaparece, lo que sugiere que el desdoblamiento del bote triple es más complicado que una flip bifurcation.