| |
Prof. Marcel G Clerc
Programa tentativo: FI7007
|
Horario: martes y Jueves(14:30-16:00)
|
|
 |
| |
Los sistemas
compuestos por muchos constituyentes microscópicos fuera
del equilibrio termodinámico exhiben una gran variedad
de comportamientos colectivos. Uno de los objetivos centrales
de la Física No-lineal es la caracterización de
estos comportamientos colectivos.
El gran éxito de
esta área de la Física en las dos ultimas décadas
no solo en las ciencias naturales como la Física, Química
y la Biología, sino también en las ciencias humanas
tales como la Sociología y la Economía, se debe
a que su objetivo principal es el estudio de fenómenos
robustos, es decir, fenómenos independientes de la Física
subyacente, por ejemplo, fenómenos ondulatorios, comportamientos
caóticos, bifurcaciones, inestabilidades y formación
de patrones.
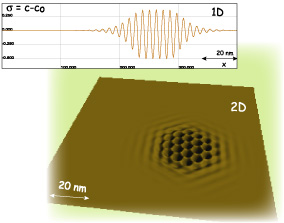
Ondas no lineales que conectan diferentes estados
de equilibrio, frentes, en sistemas disipativos extendidos han
sido observado en diferentes campos, tales como: materiales magnéticos,
cristales líquidos, corrientes filamentos en la descarga
de gas, reacciones químicas, superficie del fluido, medios
granulares, convección térmica, ondas solitarias
en óptica no lineal, diferentes poblaciones de seres vivos,
entre otros. Por lo tanto, se puede inferir la universalidad de
los Frentes.
Objetivos Principales
El objetivo principal de este curso es responder
a las siguientes preguntas :
- Caracterización de las ondas no lineales tipo frentes
en sistemas fuera del equilibrio.
- Caracterización de diferentes tipos de frentes.
- Determinación de la velocidad de Frentes.
- Mecanismo de estructuras localizadas.
- Caracterización de bifurcaciones exhibidas por estados
localizados. Aplicacion a fluidos, reaciones quimicas, medios
granulares, cristales liquidos, medios exitables, medios activos
(cavidad optica), etc.
- Interacción entre frentes.
Aplicacion a fluidos, reaciones quimicas, medios granulares,
cristales liquidos, medios exitables, medios activos (cavidad
optica), dinamica de vegetación, etc.
|
|
| |
Programa tentativo |
|
|
Out of equilibrium macroscopic systems
- Robust phenomena.
- Extended systems.
- Continuous limit of extended system.
Front propagation into unstable state
- Populations dynamics
- Determination of marginal speed: linear analysis
- Analytical profile front solution
- Stability of front solution
- Particle type behavior and interaction of fronts
- Front propagation in inhomogeneous media
- Stochastic Populations dynamics
- Front solution in reactions dynamical systems
- Pushed and pulled fronts
- Nematic-isotropic transition: pushed front
- Variational characterization of front speed
- Front propagation in discrete media
- Theoretical description of the mean speed for the discrete FKPP model
- Theoretical description of the mean speed for the Chain of dissipative coupled pendula
- Effective continuous model: oscillatory properties of front propagation
- Generalized Peierls-Nabarro potential
- Front propagation in two dimensions
- Gibbs-Thomson effect
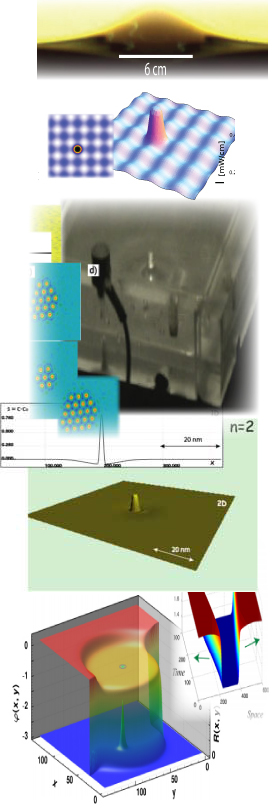
Estructuras localizadas en sistemas
Parametricos
- observaciones experimentales sistemas parametricos
- Cadena de pendulos acoplados forzados verticalmente.
- Deduccion de la Ecuacion de Schrodinger no lineal forzada
parametricamente (PDNLS)
- Solitones disipativos en PDNLS.
- interaccion de Solitones disipativos en PDNLS y verificacionexperimental.
- Solitones disipativos con armadura en una dimension
- Solitones disipativos con armadura en dos dimensiones
- Analytical explanation of velocity-curvature effect
- Dynamics around a flat interface
Front propagation into stable state
- Motivation: Simple model of Ferromagnetic transition
- Analytical characterization of front speed
- Variational systems
- Front propagation at the Freedericksz transition
- Kink interaction
- Kinematic law of a pair kinks
- Interaction of a gas of kinks: coarsegraning
- Effect of discretization kink interaction
- Localized states as result of kink interaction
- Simple model: Turing-Swift-Hohenberg equation
- Localized structures as result front interaction
- Liftshitz normal form: non variational generalization of Turing-Swift-Hohenberg Equation
- Alee effect in population dynamics: Nagumo Model
|
 |
|
Links
|
|
| |
Bibliografia
|
|
|
- Localized
States in Physics: Solitons and Patterns, Eds. o. Descalzi,
M. Clerc,S. Residori,and Assanto, G. (Springer, 2010)
- H. G. Purwins, H. U. Bodeker, and Sh. Amiranashvili, Adv. Phys.
59, 485 (2010).
- T. Ackemann, W. J. Firth, and G. L. oppo, in
Fundamentals and Applications of Spatial Dissipative Solitons
in Photonic
Devices,
edited by E. Arimondo, P. R. Berman, and C. C. Lin,
special issue of Adv. At., Mol., opt. Phys. 57, 323 (2009).
- P. Coullet, Int. J. Bifurcation Chaos 12, 2445 (2002).
- L.M. Pismen, Patterns
and Interfaces in Dissipative Dynamics
(Springer Series in Synergetics, Berlin Heidelberg, 2006),
- M. Cross and P. Hohenberg, Rev. Mod. Phys. 65,
851 (1993).
- G. Nicolis and I. Prigogine, Self-organization
in Non Equilibrium Systems (J. Wiley & Sons, New York,
1977).
- J.D. Murray, Mathematic Biology, I An Introduction, (Springer-Verlarg, New York),
- Wim van Saarloos, Front propagation into unstable states, Physics Reports, 386 29-222 (2003).
-
|
|
| |
Applet & web pages

|
|
| |
| |
. Software Interactivos |
|
| |
|
|
| |
Temas para disertar finales
- Inestabilidades
y formacion de patrones en crecimiento cristalino: Dendritas
(Miguel Escobar).
- Transicion de Ising-Bloch
en sistemas no variacionales (Guidobeth).
- Ondas de choque
y rarificacion.
- Frentes de ondas
en modelo de presas y depredadores (Roberto).
- Frentes en la reaccion
de Belousov-Zhabotinskii.
- Frentes entre un
estado homogenio y un estado caotico.
- Frentes de FKPP
entre un estado homogeneo y un patron (Eduardo).
- Propagacion de
frentes de combustion (Paulo).
- Modelos de reaccion
difusion para la invacion del cancer.
- Ruido induce propagacion
de frentes (Martin).
- Ondas no lineales
en medios excitables y espirales.
- propagacion geografica
y control de epidemias
- Frentes en dominoes.
- Frentes en cadenas
discretas opticas con acoplamiento no reciproco (Manuel).
- Transicion de pinning/depinnig
n cadenas discretas opticas con acoplamiento no reciproco
(Laura).
- Ruido sostiene
frentes en sistemas convectivos (Belen).
|
|
| |
|
|
|
|
| |
Requisitos:
Mecanica Clasica |
|
| |
Evaluacion:
tareas bi-semanales., presentaciones mensuales. El examen consistira en un seminario sobre
el analisis de un tema. |
|
|