Determinación de strain

La técnica se basa en objetos de tamaño o forma original conocida. Estos objetos se denominan marcadores de strain. La mayoría de estos marcadores cae dentro de una de las siguientes categorías.

Determinación de strain a partir de marcadores originalmente esféricos

En un campo de strain homogéneo los marcadores inicialmente circulares serán deformados en elipses, las que aparecerán en cualquier superficie cortando la roca deformada. Los ejes mayores de las elipses serán paralelos incluso para valores muy bajos de strain con los ejes de la elipse de strain.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{4cm}{\bf\hfill(Figura)}}}\end{figure}$

Las elipses representan el estado de strain en la superficie de interés específica (la que vemos). La razón entre las extensiones máxima y mínima pueden obtenerse midiendo y comparando los ejes de cualquier elipse. Lo más usual es medir un número de elipses y plotear los ejes mayores ^v/_s los menores. La pendiente de la línea que representa mejor una relación lineal (tan $\theta$ ) es la razón entre el eje mayor y el eje menor y por lo tanto, corresponde a la razón entre los strain máximos y mínimos. Si se sabe que la deformación no involucró cambio de área, los valores reales de los strains principales pueden ser determinados midiendo el área de la elipse y determinando el diámetro de la circunferencia con área equivalente. El radio de esta circunferencia será el largo inicial y los largos finales corresponderán a los largos de los ejes de la elipse de strain. La extensión se puede determinar:

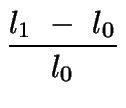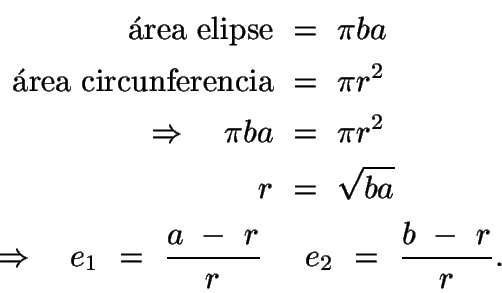
$\begin{displaymath}\begin{split} \text{\'{a}rea elipse}\ &=\ \pi ba\\ \text{\'{... ...frac{a\ -\ r}{r}\ \ &\ \ e_2\ =\ \frac{b\ -\ r}{r}. \end{split}\end{displaymath}$

Determinación de strain a partir de marcadores originalmente elipsoidales

En el caso anterior, todas las elipses tenían ejes máximo y mínimo paralelos entre sí y paralelos a los ejes de la elipse de strain. Cuando los marcadores son elípticos esto no se cumple, a menos que el eje mayor de la elipse no deformada coincida con la extensión principal.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{8cm}{\bf\hfill(Figura)}}}\end{figure}$

Generalmente existirá un ángulo $\phi$ entre el eje mayor de la elipse de strain (extensión principal) y el eje mayor de la elipse deformada (partícula). Este ángulo se conoce como fluctuación y tiende a decrecer con un aumento de strain (a mayor deformación, las orientaciones tienden a ser paralelas).

El problema de determinar el strain de partículas originalmente elípticas se observa en (c); una partícula originalmente elíptica con una razón axial igual a R₀ = ${\frac{{\text{eje mayor}}}{{\text{eje menor}}}}$ , inclinada a un ángulo $\theta$ de la dirección de máxima extensión. La elipse de strain tiene una razón R_s entre sus ejes.

El resultado de la deformación es una partícula elíptica, de razón axial R_f, inclinada a un ángulo $\phi$ de la dirección de extensión máxima.

En la figura anterior (b) se puede ver que la forma final R_f depende de la orientación relativa de la partícula original y del strain aplicado. Cuando ellos interfieren constructivamente (i), la elipse resultante tiene la mayor excentricidad y cuando ellos interfieren destructivamente (ii), la elipse tiene la menor excentricidad.

Entonces, cuando una elipse con elipticidad R₀ es deformada homogéneamente, la forma resultante es también elíptica. La forma de esta elipse final R_f, es función de cuatro factores:

La figura siguiente muestra una superficie que contiene un número de partículas elípticas de forma constante R₀ = 2, orientada a distintos ángulos de un marcador inicial de dirección paralela al eje x ( $\theta$ = 90⁰, $\theta$ = 75⁰, $\theta$ = 60⁰, 45⁰, 30⁰,5⁰ y 0). El gráfico muestra R₀ = constante ^v/_s $\theta$ .

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{8cm}{\bf\hfill(Figura)}}}\end{figure}$

Cuando se superpone un strain homogéneo (B), con elipse de razón R_s = 1, 5, entonces las elipses iniciales cambian dependiendo de la orientación con respecto a la orientación de los ejes de la elipse de strain. La orientación de las elipses también cambia ( $\phi$ ), excepto para $\theta$ = 90⁰ y $\theta$ = 0. Los ejes mayores de las elipses tenderán a ubicarse paralelos al eje mayor de la elipse de strain.

La elipse inicial que tiene eje mayor paralelo a la elongación principal máxima ( $\theta$ = 0) tomará una nueva forma que será más elíptica que la elipse de strain. Mientras que la elipse inicial ubicada a $\theta$ = 90⁰ se volverá menos elíptica que la elipse de strain.

Las elipticidades R_f de todos los otros marcadores elípticos se encuentran entre ambos valores, pero la mayoría tendrá elipticidad mayor que la elipse de strain.

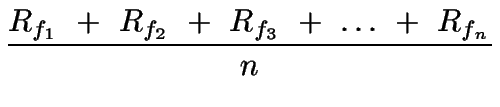( $\displaystyle {\frac{{R_{f_1}\ +\ R_{f_2}\ +\ R_{f_3}\ +\ \ldots\ +\ R_{f_n}}}{{n}}}$ )

R_{f_max}	=	R_s R_{0_max}	$\displaystyle \Rightarrow$	$\displaystyle \sqrt{{R_{f_{max}}R_{f_{min}}}}$	=	R_{0_max}
R_{f_min}	=	$\displaystyle {\frac{{R_{0_{max}}}}{{R_s}}}$	$\displaystyle \Rightarrow$	$\displaystyle \sqrt{{\frac{R_{f_{max}}}{R_{f_{min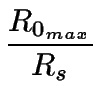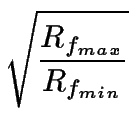}}}}}$	=	R_s.

Entonces, para determinar el strain R_s y la forma original R₀ es necesario establecer R_{f_min} y R_{f_max} y resolver las ecuaciones.

Para hacer esto, se puede tomar una cara (o fotografía de una cara) que contenga los marcadores de strain elípticos. Se mide la razón R_f de cada elipse, R_f = ${\frac{{\text{eje mayor}}}{{\text{eje menor}}}}$ y la orientación $\phi$ = ángulo entre la línea dato y la dirección de extensión principal. (Son las fluctuaciones).

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{5cm}{\bf\hfill(Figura)}}}\end{figure}$

Las fluctuaciones de cualquier elipse pueden ser obtenidas del gráfico, midiendo el ángulo entre la línea de simetría y el punto en la curva que representa la elipse deformada.

Determinando valores R_{f_max} y R_{f_min} (puntos 2 y 1 del gráfico) se determina posteriormente los valores de R₀ y R_s.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{5cm}{\bf\hfill(Figura)}}}\end{figure}$

Si la magnitud de la forma original R₀ es mayor que el strain aplicado R_s, entonces los datos no forman una curva cerrada sino una curva en forma de campana.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{5cm}{\bf\hfill(Figura)}}}\end{figure}$

(En este ejemplo las fluctuaciones máximas son de 180⁰.) Se ha asumido, además, que las partículas originales tienen la misma forma original R₀. En la práctica esto no es común, sino que hay un rango para R₀. En este caso se obtendrá una curva cerrada para cada valor R₀ o rangos entre R₀.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{5cm}{\bf\hfill(Figura)}}}\end{figure}$

Por otra parte, del gráfico R_f ^v/_s $\phi$ puede ser detectada la existencia de orientaciones preferenciales de las partículas no deformadas. Las orientaciones preferenciales tienden a formar gráficos R_f ^v/_s $\phi$ asimétricos.

Marcadores con simetría bilateral

En general, la simetría bilateral que tienen algunos fósiles es destruida durante la deformación, a no ser que el eje de simetría coincida con una de las direcciones principales de strain.

La relación original del ángulo recto se pierde y el cambio en ángulo da una medida del cizalle angular ( $\psi$ ) y por lo tanto, se puede determinar el strain de cizalle que sufrieron las líneas A y B, originalmente perpendiculares.

Los valores de $\psi$ en esas dos direcciones tienen la misma magnitud, pero signo opuesto.

$\begin{figure}\noindent\centering\fbox{\parbox{.95\linewidth}{\rule[-0cm]{0mm}{5cm}{\bf\hfill(Figura)}}}\end{figure}$

Determinación de strain a partir de un marcador de largo original conocido

A diferencia de los marcadores ya discutidos, los belemnites no tienen las mismas propiedades que la matriz rocosa. Se asume que ellos tienen un comportamiento frágil durante la deformación y que los segmentos no cambian de largo. Si esto es verdad, la suma de los fragmentos da el largo originall l_o; el largo final se obtiene directamente midiendo su largo l en la roca deformada. Con estos datos se obtiene la extensión en distintas direcciones.