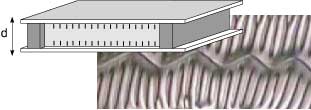
Los sistemas compuestos por muchos constituyentes fuera del equilibrio termodinámico exhiben una gran variedad de comportamientos colectivos espaciales y temporales. Uno de los objetivos capitales de la Física No-lineal es la caracterización de estos comportamientos colectivos.

El gran éxito de esta area de la Física contemporanea en las dos últimas décadas no sólo en las ciencias naturales como la Física, Química y la Biología, sino también en las ciencias humanas tales como la Sociología y la Economía, se debe a que su objetivo principal es el estudio de fenómenos robustos, es decir, fenómenos independientes de la Física subyacente, como por ejémplo, fenómenos colectivos, comportamientos caóticos, bifurcaciones, inestabilidades y formación de patrones (patterns). Entonces estos fenómenos son universales, como lo ilustra la formación de patrones regulares en medios disipativos tales como aquellos observados en sistemas químicos, descarga de gases, laseres, plasmas, cristales líquidos, medios granulares, crecimientos de cristales, fluidos, electroconvección, pigmentación de los animales e insectos, etc.

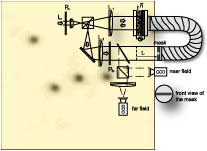
El objetivo principal de este curso es responder a las tres siguientes preguntas :

• Caracterización de las soluciones estacionarias o estados extendidos exhibidas por sistemas fuera del equilibrio: estados uniformes, patrones (espacio temporales). Aplicación a fluidos, reaciones quimicas, medios granulares, cristales liquidos, medios exitables, medios activos (cavidad optica), etc.
• Caracterizacion de bifurcaciones exhibidas por estados extendidos. Aplicación a fluidos, reaciones quimicas, medios granulares, cristales liquidos, medios exitables, medios activos (cavidad optica), etc.
• Descripcion unificada de estas bifurcaciones, por metodos de ecuaciones de solubilidad (Ecuaciones de amplitud y de fase, forrmas normales y metodos de multiescala). Aplicación a fluidos, reaciones quimicas, medios granulares, cristales liquidos, medios exitables, medios activos (cavidad optica), etc.
• Formación de estructuras compuestas por estados extendidos, frentes, estructuras localizadas, defectos (Soluciones tipo partícula). Caracterizacion de los mecanismo de propagación. Aplicación a dinámica de poblaciones, fluidos, reaciones quimicas, medios granulares, cristales liquidos, medios exitables, medios activos (cavidad optica), etc.

• H. D. Abarbanel, M.I. Rabinovich and M.M. Sushchik, Introduction to Nonlinear Dynamics for physicists (World Scientific Publishing, Singapore,1993).
• A. Newell and J. Moloney, Non-linear Optics, Addison-Wesley, Redwood, CA 1992.
• Paul Manneville, Instabilities, Chaos And Turbulence: An Introduction To Nonlinear Dynamics And Complex Systems
• J. Guckenheimer and P. Holmes, Nonlinear oscillations, dynamical systems and bifurcations of vector fields.(Springer-Verlarg, New York, 1983).
• M. Cross and P. Hohenberg, Rev. Mod. Phys. {\bf 65}, 851 (1993).
• J.D. Murray, Methematical Biology, I An Introduction, (Springer-Verlarg, New York, 2002).
• P.G. Drazin, Nonlinear Systems, (Cambridge Texts in Applied Mathematics, 1992).
• S. Chandrasekar, Hydrodynamic and hydromagnetic instability (Clarendon Press, Oxford 1961).