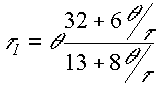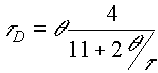SINTONIZACIÓN
DE CONTROLADORES
¿Qué
valores de los parámetros usar?
-
Usar Criterios
simples (tasa de decaimiento de oscilaciones de 1/4; mínimo tiempo
de estabilización; minimización de error; etc) que arrojan
varios conjuntos distintos de parámetros (luego, ¿cuál
conjunto usar?)
-
Usar criteios de minimización de
integrales del error ( p.e. ISE, ITAE, IAE) que un tanto enredado y extenso.
-
Utilizar
los parámetros que resultan de observaciones y reglas semi empíricas
que, en la práctica, han funcionado bien.
El
método semi empírico de mayor popularidad, conocido como
MÉTODO
DE LA CURVA DE REACCIÓN
desarrollado
por Cohen y Coon [Trans. ASME, 75, 827, (1953)] considera un sistema cuyo
bucle de control ha sido "abierto" mediante la desconección del
elemento final de control desde el controlador (es decir, la señal
de control "c" es manejada por el diseñador, es decir, usted, y
no por el controlador). El bucle "abierto" corresponde al diagrama siguiente:
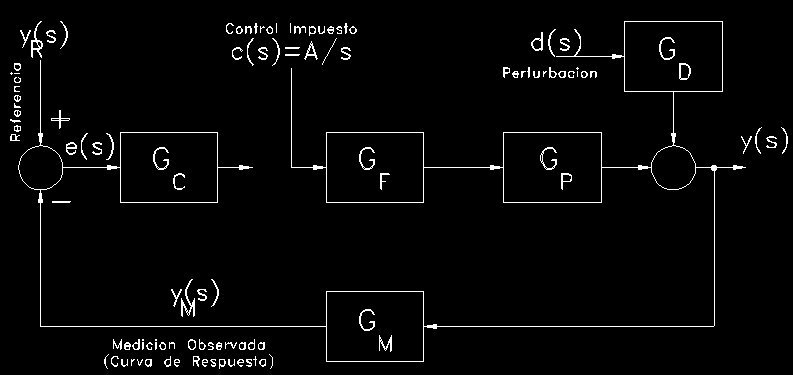
Si
el diseñador introdujese una señal "c"
(en variable desviación) consistente en un escalón de amplitud
"A" (es decir,
la función A/s
en el campo Laplace, tal como se muestra en la línea "cortada",
bajo el rótulo "control impuesto") el actuador final de control
(p.e. el vástago de una válvula actuada) recibiría
un brusco cambio de posición.
Si
se registra la medición de la salida "yM(t)"
en el tiempo se obtendrá la curva
de reacción del proceso
(o del sistema).
La
relación entre "yM"
y "c" define
la función de transferencia de la curva de reacción, que
suele ser del siguiente tipo:
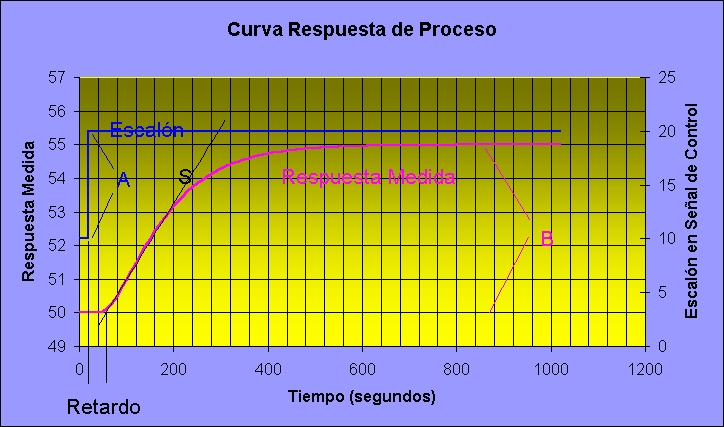
y que corresponde a la función
de transferencia que relaciona la señal de control impuesta con
la respuesta medida (observe que la perturbación, "d", permanece
constante en este análisis):
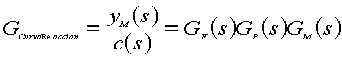que destaca
que la C.R.P. está afectada por las dinámicas del sensor
y del elemento final de control y no sólo por la dinámica
del proceso.
El
gran aporte de Cohen y Coon fue destacar que para muchos procesos observados
(se agregaron más observaciones después) la respuesta es
sigmoidea y puede ser bien modelada por un primer orden con retardo:
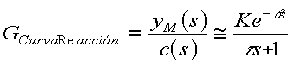con
3 parámetros fáciles de estimar:
K=
Ganancia estática, la razón entre el cambio de la respuesta
a la magnitud del escalón ("B/A")
t=Tiempo
de respuesta, dado por la razón de B
a la pendiente máxima lineal de la respuesta, S
q=Tiempo
de retardo, dado por el corte de un primer orden en el eje tiempo.
¿Son
estos Parámetros (primer orden con retardo) Fáciles de Estimar?
La
gráfica de la Curva de Reacción de un proceso (es decir,
se modificó la señal de control al proceso y se observó
la medición de la respuesta en un bucle "abierto") muestra la definición
de los parámetros descriptivos más evidentes (A,
B
y S).
Si bien la curva se generó
sin ruido (para simplificar la discusión), permite observar que:
B,
el valor final de la respuesta observada "yM(t)"
es 5;
A,
la amplitud del escalón en la señal de control "c(t)" es
10;
S,
una aproximación al valor de la pendiente, es 0.023;
de modo que:
K=B/A=0,5
t=B/S=220
segundos
q=40
segundos
Finalmente, Cohen
y Coon aplicaron los criterios simples (1/4 de decaimiento; minimización
de offset y minimización de ISE) para obtener los "mejores" valores
de los parámetros del controlador en bucle cerrado.
El detalle de desarrollo
es un ejercicio de minimización (que los estudiantes bien pueden
desarrollar) que arroja un conjunto de valores "recomendables" para los
parámetros de cualquiera de los tres tipos de controlador (i.e.
"P", "PI" o "PID"):
| |
KC
|
tI
|
tD
|
| P |
 |
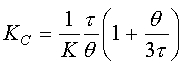No Aplicable |
No Aplicable |
| PI |
 |
 |
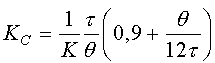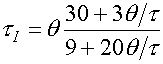No Aplicable |
| PID |
 |
 |
 |
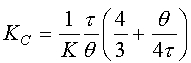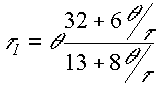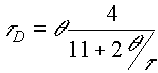Estos valores de las constantes
de los controladores corresponden al criterio de
Cohen y Coon; pero son más conocidas como las constantes
del método de la curva de reacción; e incluso, como
las constantes del método de abrir el bucle
(si bien este término resulta demasiado coloquial)