Introducción: El Mecanismo de Realimentación (feedback).
¿Por qué debemos controlar las unidades de proceso?
Sistema de Control.
Elementos de diseño de un controlador de una operación.
Modelamiento de la Dinámica de Procesos.
¿Cómo reducir el Número de Grados de Libertad?

Introducción: El Mecanismo de Realimentación (feedback).

Es posible observar mecanismos de realimentación muy frecuentemente en la naturaleza, tanto como en aplicaciones tecnológicas:

• La capacidad de los mamíferos de caminar, no sólo los bípedos, depende de un mecanismo de realimentación de la información de la posición del cuerpo 
• La mantención de la temperatura del cuerpo, dentro de una banda de las décimas de grado cuando la temperatura exterior cambia en decenas de grados, no sería posible sin tal mecanismo 
• La orientación de las hojas de un vegetal hacia el sol se basa en realimentación 
• Cuando se desea mantener la temperatura de un horno de fundición, se recurre a la realimentación 
• Etc., etc.

Habitualmente se puede representar un proceso por una caja que engloba las propiedades del proceso (diagrama en bloques). Dado un proceso H, este se dice afectado por una entrada u (excitación) para producir una salida y (respuesta) que es el resultado de la acción de H sobre u para entregar y. En síntesis, y=Hu.

Por ejemplo, si el proceso H fuese el juego de las bolitas (gochitas para los sureños), entonces u sería el impulso entregado por la mano del jugador a una bolita e y sería la dirección que adquiere la misma. Naturalmente, el juego es difícil si se debe acertar a impactar a otra bolita del jugador antagónico, que está en otras coordenadas y el suelo es irregular. Una ves que el jugador ha aplicado u, la suerte está echada y no hay más que hacer que esperar el resultado. Esta manera de manejar el proceso H se denomina control de bucle abierto, porque no existe relación alguna de y a u.

Se podría pensar en una pequeña triquiñuela en este juego, consistente en construir una bolita especial. La bolita "trucada" dispondría de un sistema que le permita observar la posición de la bolita a que debe impactar, de un mecanismo de cálculo de "¿cómo voy?" (es decir del error, en términos de "muy a la izquierda" o "muy a la derecha") y de un mecanismo de modificación de su trayectoria. En estas condiciones, el jugador entrega un impulso u cualquiera y la bolita, dotada ahora de un mecanismo de reacción al error de trayectoria, asegurará el éxito de cada jugada (ya no sería un juego, ¡claro!). El jugador, en estas condiciones, es sólo un elemento actuador, que entrega un impulso, mientras que la entrada al proceso en bucle cerrado, es la dirección deseada (es decir, a que bolita se debe impactar).

Un bucle cerrado por realimentación negativa está compuesto por un entrada y_REF que especifica la respuesta deseada, por un mecanismo de resta de la respuesta observada, que calcula así el error e, de un amplificador K que transduce la señal de error en una acción u sobre el proceso, del proceso H que produce la salida y y de una línea que transporta la información acerca de y hacia el restador de cálculo del error e. Los diversos diagramas se observan en la página siguiente.

Para un proceso cualquiera, en que la relación de entrada a salida fues un simple proporcionalidad (dada precisamente por H), el proceso responderá con y=Hu, el amplificador responde según u=Ke, y el comparador evalúa el error según e=y_REF-y, de modo que se puede despejar la respuesta y que queda:

donde debiera resultar evidente que es sólo cuestión de elegir una ganancia K del amplificador de error suficientemente grande (es decir que HK sea mucho mayor que 1) para asegurar que la salida es tan cercana como uno quiera a la deseada.

¡Ese es el efecto del mecanismo de realimentación!

Es claro, al decir de Bernard Friedland, que si H fuese siempre tan simple como una relación de proporcionalidad, no necesitaríamos este curso. Además, para un ingeniero de procesos químicos, tal relación entre entrada y salida es prácticamente inexistente (no así para un ingeniero eléctrico).

Uno de los principales problemas en procesos es la presencia de "retardos", es decir, se puede modificar la concentración de un caudal de entrada pero su efecto tardará en observarse.

Por otra parte, usando las relaciones anteriores, es simple observar el efecto de un simple retardo.

Si, por ejemplo, el proceso es de ganancia unitaria (H=1) pero retardada en t unidades de tiempo t entonces y(t)=u(t-t ), entonces

de donde y(t)= K[y_REF(t-t )-y(t-t )]

Para analizar la respuesta dinámica de sistemas originalmente en estado estacionario, se suelen imponer ciertas entradas típicas: cambios en escalón, impulsos o señales oscilatorias. En este caso, se elegirá un cambio escalón.

Sea, entonces, el sistema en estado estacionario en tiempo cero, con la referencia y la salida en cero. A tiempo cero, se cambiará la referencia de cero a uno. Naturalmente, no habrá efecto ninguno en la salida durante t unidades de tiempo. Sin embargo, durante el intervalo de cero a t si que existe una entrada u al proceso, dada por u(t)=K(1-0)=K. En el intervalo entre t y 2tla salida existirá efectivamente, y tendrá el valor y=K.

Este cambio (retardado) de la salida y se refleja (de inmediato) en el comparador y por ende, en la excitación u del proceso. Así, el proceso será excitado, durante las siguientes t unidades de tiempo (es decir para t entre t y 2t ) por

El alumno podrá demostrar que, después de n intervalos de duración t la respuesta será

y(t)=K-K²+K³+ .... + (-1)^n-1K^n-1 que, si K es menor que 1 permitirá que y(t) converja eventualmente a

Por otra parte, si K=1, la salida cambia entre cero y uno cada t unidades de tiempo. Finalmente, si K es mayor que uno, la salida diverge. Aún más, aún cuando converge, no llega al valor deseado (que era 1)!

Así las cosas, es evidente que la presencia de un simple retardo imposibilita la consecución del objetivo buscado.
 

¿Por qué debemos controlar las unidades de proceso?

Mantención del punto de operación

• Si un proceso (una Planta) es visto como un conjunto de operaciones (equipos) inteligentemente conectadas, entonces la mantención del punto de operación del proceso global (la Planta) se podría satisfacer manteniendo una consigna determinada en cada operación. El punto de operación requerido puede ser simple (un cierto pH o una cierta temperatura) o complejo (una cierta rentabilidad).

• Seguridad (Presión, Temperatura, Composición, etc entre un máximo y un mínimo de seguridad) 
• Especificaciones (es decir, control de la calidad de una variable ; no sólo cantidad) 
• Regulación Ambiental (efluentes, emisiones, residuos sólidos) 
• Restricciones operacionales para cada equipo u operación (alturas de tanques, potencias a las bombas, etc) 
• Economía óptima (frente a materiales cambiantes, energías a tarifa cambiante, etc.)

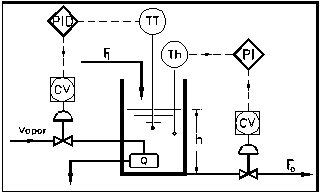La mantención de nivel y temperatura de un simple tanque está sujeta a perturbaciones en la temperatura de entrada del vapor y el caudal de carga al tanque.
 

Sistema de Control.

Conjunto racional y sistemático de equipos (sensores, actuadores, amplificadores, computadoras, algoritmos, etc.) e intervención humana (diseñadores y operadores de proceso) que permite operar el sistema controlado (una planta, p.e.) con asistencia del sistema de control mismo.

Se distinguen 3 CLASES generales de requerimientos que se satisfacen con sistemas de control:

1. Eliminar la influencia de perturbaciones externas
2. Asegurar la estabilidad del proceso
3. Optimizar el proceso

Elementos de diseño de un controlador de una operación.

¿Qué hacemos para diseñar?

1. Definir los Objetivos de control, es decir:
1. Asegurar estabilidad
2. Suprimir influencias de perturbaciones externas
3. Optimizar el rendimiento económico
4. combinación de a), b) y c)
Comenzamos con definiciones más bien cualitativas que, progresivamente, se expresan cuantitativamente; usualmente, los objetivos se expresan cuantitativamente para variables de salida (respuestas). (e.g. T= T_ref± 5%,etc.)
2. Especificar qué variables se deben medir para monitorear la operación a controlar, e.g.:
1. Medir directamente las variables que figuran en el objetivo de control, las que se definen como mediciones primarias, o
2. Medir variables que permitan deducir las variables que figuran en el objetivo de control. Estas variables se definirán como mediciones secundarias mientras que el valor de las variables del objetivo control serán variables inferidas.
3. Seleccionar las variables Manipuladas.
1. Del conjunto de variables de entrada, ¿cuáles permiten controlar el proceso?
4. Seleccionar la Configuración de Control
1. La configuración de control especifica cómo se conecta la información medida con las variables manipuladas.
2. una misma información (e.g. temperatura) puede dirigirse a dos variables manipulada distintas (e.g. Calor de calefacción o Tasa de reciclo de destilado).
3. La configuración más típica es de realimentación (feed back)
5. Determinar cómo las mediciones permiten ajustar los objetivos de control
1. Se define el manejo de la información (mediciones) necesario para concluir la acción necesaria sobre las manipuladas.

Modelamiento de la Dinámica de Procesos.

Si se debe eliminar la influencia de perturbaciones o asegurar la estabilidad u optimizar un proceso es posible concebir el (o los) mecanismos para conseguir el objetivo a través de conocer cuantitativamente el comportamiento del proceso. Tal capacidad de conocer cuantitativamente un proceso se suele desarrollar mediante el modelamiento.

Los modelos pueden ser de variados tipos, cada uno asociado a una función útil :

• Modelos icónicos 
• Modelos a escala (maquetas) 
• Modelos conceptuales (teorías científicas) 
• Modelos matemáticos

Para el control de procesos, se recurre a modelos conceptuales y a modelos matemáticos.

En general, los modelos matemáticos se construyen, de preferencia, basados en un modelo conceptual probado y confiable. En particular, recurrimos a leyes de conservación y a balances dinámicos.

donde "S" puede ser:

• Masa Total 
• Moles 
• Energía Total 
• Cantidad de Movimiento

expresión de sobrada utilidad en Ingeniería Química.

En cambio, si se analiza el modelo diferencial se utiliza aceptando que "S" varía en el sistema, se habla de MODELO DINÁMICO.

Un simple ejemplo se pude obtener de un estanque calefaccionado.

Aún cuando buscamos un modelo dinámico, se mantendrán las hipótesis simplificatorias más típicas, a saber

• Agitación perfecta 
• Area constante 
• Densidad constante 
• Calor disponible instantáneo e independiente de T

MODELO:

Ecuación Dinámica de la Masa, en términos de las variables observables:

BALANCE de ENERGIA

donde T^* es una T de referencia. Si es un líquido, entonces dH se aproxima bien a dE.

que, despejado y en función de las variables medibles arroja:

¿Cual sería el modelo dinámico?

¿Es natural que se obtengan dos ecuaciones modelo? ¿Por qué?

¿Cómo incide el modelo en la regulación (control) de la temperatura del tanque (o de salida)?

¿Qué se puede decir de la utilidad del modelo dinámico?

Al modelar se obtiene un número (E) de ECUACIONES MODELO, que especifican interrelaciones entre un número (V) de VARIABLES físicas, químicas, termodinámicas, bioquímicas, etc.

El RPA calefaccionado es descrito por 2 ecuaciones y tiene 6 variables: h, T_S, F_e, F_S, T_e, Q, suponiendo que el área de sección, la densidad y el calor específico son constantes y que tienen un valor dado.

En estas condiciones, V>E, lo que significa que existen MULTIPLES soluciones al sistema, es decir, se pueden elegir libremente (V-E) valores de variables y cada elección genera una solución distinta.

Dado que se eligen libremente este número de variables, se define el número de GRADOS DE LIBERTAD f=V-E

El RPA calefaccionado tiene f=4

Para especificar completamente un sistema, f debe ser cero, de modo que exista una única solución.
 
 

¿Cómo reducir el Número de Grados de Libertad?

1.- Examinando nuevas relaciones:

En el RPA calefaccionado se suele dar el caso que la salida es una función de la pérdida de carga y la altura (estanque de cabeza). En estas condiciones, se ratifica que F_S=b·Ö h (con b coeficiente constante).

Dado que existe una relación física (Bernoulli) entre dos de las 6 variables, se agrega una ecuación y se reduce f en 1.

2.- Incorporando Bucles de Control:

El bucle de control feed back de nivel, donde se instala un transmisor de nivel (Th) que regula la válvula de la salida mediante un controlador proporcional e integral ("PI") produce una relación entre el caudal de salida (F_S) y el nivel del tanque (h):

mientras que el bucle de temperatura implementa una relación proporcional, integral y diferencial ("PID") entre la temperatura y el calor cedido por regulación del flujo de vapor:

de manera que cada bucle reduce un grado de libertad.

Es posible, entonces, concluir que si dos bucles de control reducen en dos el número de grados de libertad del sistema RPA calefaccionado, quedan dos grados de libertad definitivos.

Esta observación es consecuencia de las características de proceso del equipo:

• El caudal de entrada, F_e, es determinado por procesos aguas arriba, de modo que es una perturbación al sistema. 
• La temperatura de entrada al sistema, T_e, está determinada por condiciones externas al proceso y es una segunda perturbación al sistema.

El tanque calefaccionado podría operar a nivel constante, es decir, F_S=F_e, en cuyo caso sólo sería necesario modelar la energía del sistema, en tal caso:

, pero Q sería

, es decir,

o, más bien, 

con 

El modelo se resuelve fácilmente para estado estacionario y permite encontrar valores (indicados por subíndice "e.e.") que se utilizan para establecer las variables "desviación" respecto del estado estacionario. Así, la MISMA estructura de la ecuación anterior es válida para variables desviación, indicadas por una "prima" en el superíndice:

, arreglo que resulta útil pues los valores iniciales serán cero.

Si se transforman ambos lados por Laplace:

que genera 2 funciones de transferencia de modo que:

Cada función de transferencia representa la reacción dinámica del sistema a un cambio en cada una de las variables de entrada; en particular, es posible visualisar el proceso de obtención de las funciones de transferencia como aquellas que se obtienen cuando cambia UNA variable de entrada (y, dado que están en variable desviación, la otra entrada es nula) arroajndo así cada una de las funciones de transferencia por separado. Dado que el modelo es lineal, la respuesta dinámica completa es la simple suma de las respuestas por separado.

Es decir, para un modelo con dos variables de entrada y una de salida, se obtienen 2 funciones de transferencia, que explican el comportamiento de la salida. Es posible, entonces, diagramar en bloques este modelo de entrada/salida.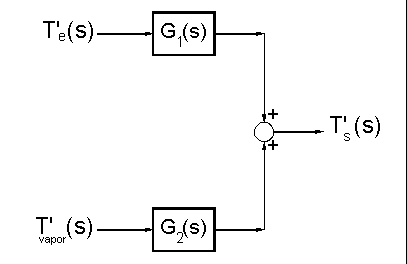

Estas funciones de transferencia son, obviamente, funciones complejas de la variable compleja "s". El alumno debe notar que para UN solo proceso se obtuvieron DOS funciones de transferencia y ADEMAS, el denominador de ambas es el mismo; en particular "s+a".

CONTINUACION