Reología

(Twiss y Moores, 1992; Price y Cosgrove, 1990)

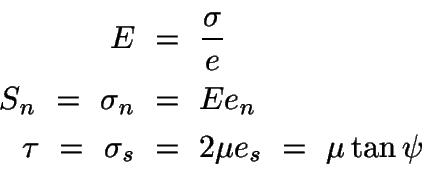
En esta parte del curso consideraremos las relaciones entre stress y strain que son útiles para describir el comportamiento de las rocas a escala macroscópica. A esta escala se considerará la roca como un medio continuo, es decir, las anisotropías y heterogeneidades asociadas a su naturaleza policristalina no son consideradas. Se establecerá un grupo de relaciones matemáticas que son útiles para describir el comportamiento mec'anico de diferentes tipos de rocas a diferentes temperaturas, stresses y presiones.

Reología se refiere a la deformación y flujo de cuerpos ideales.

Diferentes materiales se comportan de manera distinta cuando son sometidos a un mismo estado de stress. Por ejemplo, en compresión uniaxial un tipo de material puede sufrir un pequeño acortamiento y luego estabilizarse, mientras que otro puede fluir continuamente. Nosotros podemos expresar estas diferencias matemáticamente se podemos calcular la respuesta del material frente al stress.

Modelos continuos del comportamiento de los materiales

Materiales elásticos

Una de las ecuaciones stress-strain más simples y probablemente más familiar es para sólidos elásticos. Este tipo de material se deforma proporcionalmente al stress aplicado. Cuando el stress es retirado el material vuelve a su estado original no deformado y la deformación se dice recuperable. La relación es representada por una ecuación lineal

$$\begin{split} E\ &=\ \frac{\sigma}{e}\\ S_n\ =\ \sigma_n\ &=... ...\\ \tau\ =\ \sigma_s\ &=\ 2\mu e_s\ =\ \mu\tan\psi \end{split}$$

que dice que un stress normal es proporcional a la extensión o que el stress de cizalle es proporcional al strain de cizalle.

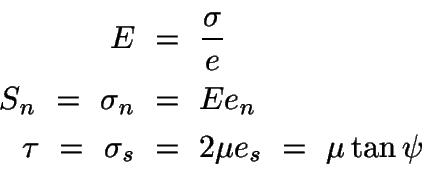
La constante E es el Módulo de Young, E  =  ${\frac{{\sigma_n}}{{e_n}}}$, como e_n es adimensional, la unidad de este módulo es la misma que la de $\sigma_{n}^{}$, es decir, ${\frac{{kN}}{{m^2}}}$ o Pa. $\mu$ es el Módulo de cizalle o Módulo de rigidez, $\mu$  =  ${\frac{{\tau e_s}}{{2}}}$ o G  =  ${\frac{{\tau}}{{\tan\psi}}}$.

Algunos autores definen:

$$\tau$$  =  2$$\mu$$es		$$\gamma$$  =  tan$$\psi$$
$$\tau$$  =  $$\mu$$$$\gamma$$		es  =  $${\frac{{1}}{{2}}}$$tan$$\psi$$
$$\mu$$  =  $${\frac{{\tau}}{{\gamma}}}$$		G  =  $${\frac{{\tau}}{{\gamma}}}$$
	$$\Rightarrow$$    $$\mu$$  =  G.

El módulo de rigidez es para la definición por cizalle simple.

Las rocas más resistentes muestran un valor de E alto (gran pendiente). En la práctica, las rocas no siempre tienen una relación stress-strain lineal. Sin embargo, la desviación es pequeña y uno puede, para la mayoría de las rocas, encontrar un módulo elástico (E) conveniente.

Las rocas más blandas tienen menor resistencia y tienden a mostrar una relación stress-strain no lineal con una concavidad inicial debido al cierre de poros o de microfracturas y una zona final convexa cuando se acerca la ruptura. En ambas partes de la curva parte de la energía es irrecuperable. Entre las zonas mencionadas la curva tiene una relación stress-strain lineal. En mecánica de rocas, los valores de E usados en este tipo de rocas es determinado en la parte recta (lineal) de la curva.

Roca		E (MPa)
Cuasi-elástica	(muy resistente)	>  8000
Semi-elástica	(resistente, dura)	4000 - 8000
	(moderadamente resistente)	2000 - 4000
No elástica	(débil)	1000 - 2000 -
	(muy débil)	<  1000

Otros valores que pueden tener importancia en condiciones estáticas o dinámicas particulares son el Módulo tangente, que corresponde a una recta tangente a la curva o el Módulo secante, que es la pendiente de una recta trazada desde el origen a un punto en la curva; usualmente se elige este punto como el punto de ruptura o el 50% del valor de ruptura.

El stress S_n causa, además de un acortamiento en la dirección z, un strain extensivo horizontal tal que e_x  = I>e_y. Este efecto fue determinado por Poisson, quien expresó la razón entre los strains horizontales y el vertical resultantes de un stress uniaxial como una segunda constante del material:

$${\frac{{\vert e_x\vert}}{{\vert e_z\vert}}}$$  =  $${\frac{{\vert e_y\vert}}{{\vert e_z\vert}}}$$  =  $$\nu$$

donde $\nu$ es la razón de Poisson, además

$${\frac{{1}}{{\nu}}}$$  =  m

donde m es el número de Poisson.

$\nu$ y m son adimensionales.

La teoría elástica considera $\nu$ y m como constantes. Sin embargo, las rocas, al ser un agregado de partículas y no presentar una relación stress-strain totalmente lineal, muestran también valores de $\nu$ ligeramente diferentes a diferentes rangos de stress.

Consideremos ahora un sistema de stress en tres dimensiones. Sabemos que cada uno de los stresses produce acortamiento en la dirección de aplicación y un estiramiento en las dos direcciones ortogonales y que ellas se relacionan:

$${\frac{{e_z}}{{e_x}}}$$  =  $${\frac{{e_z}}{{e_y}}}$$  =  m,

entonces

e_y  =  e_x  =  $${\frac{{e_z}}{{m}}}$$,

pero además

$$\begin{split} &S_z\ =\ Ee_{S_{z}}\\ &e_{S_{z}}\ =\ \frac{S_z}{E}\\ &e_x\ =\ e_y\ =\ \frac{S_z}{mE}. \end{split}$$

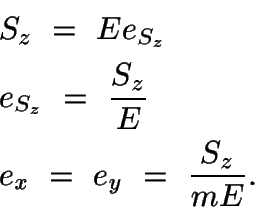
Cada stress principal contribuirá a un strain total en la dirección z. El stress principal S_z producirá un componente de strain e_z', dado por

e_z'  =  $${\frac{{S_z}}{{E}}}$$

(análogo al caso uniaxial).

Los stresses horizontales principales, S_x y S_y, producirán cada uno un alargamiento en el eje z, dados por

e_z''  =  $${\frac{{S_x}}{{mE}}}$$

y

e_z'''  =  $${\frac{{S_y}}{{mE}}}$$.

Como todos los stresses son compresivos, los componentes extensivos del strain tendrán signo opuesto al signo de e_z'. Así, el strain total en el eje z es

$$\begin{split} e_z\ &=\ e_z'\ -\ e_z''\ -\ e_z'''\\ &=\ \frac... ... &=\ \frac{1}{E}[S_y\ -\ \frac{1}{m}(S_x\ +\ S_y)]. \end{split}$$

Utilizando el mismo método se puede obtener e_x y e_y:

$$\begin{split} e_x\ &=\ \frac{1}{E}[S_x\ -\ \frac{1}{m}(S_y\ +... ... &=\ \frac{1}{E}[S_y\ -\ \frac{1}{m}(S_x\ +\ S_z)]. \end{split}$$

Este set de ecuaciones permite, por ejemplo, bajo razonables supuestos, establecer la relación entre el stress horizontal y el vertical cuando la corteza está sujeta sólo a la fuerza de gravedad.

Supongamos una columna en la corteza, con relieve despreciable, que está sujeta a una carga gravitacional. Supongamos además que es strain lateral es cero (e_x  =  e_y  =  0). Un pequeño cubo dentro de la corteza estará sujeto a un stress vertical (S_z) como resultado del peso de los estratos que le sobreyacen. Por conveniencia supondremos que las propiedades son uniformes en toda la columna. El stress vertical será

S_z  =  $$\rho$$gz   o   S_z  =  $$\gamma$$z

donde $\rho$ es la densidad del material y $\gamma$ es el peso específico del material $\gamma$  =  $\rho$g. g es la constante gravitacional (g  =  9, 8${\frac{{m}}{{s^2}}}$) y z es la profundidad a partir de la superficie.

Si asumimos además que la roca es completamente elástica, entonces el stress vertical tenderá a producir un strain lateral. Pero inicialmente asumimos que el strain lateral es cero, lo que significa que existe un stress horizontal que cancela el efecto producido por S_z (S_h  =  S_x  =  S_y):

e_x  =  e_y  =   0

S_x  -  $${\frac{{1}}{{m}}}$$(S_y  +  S_z)  =   0

pero

S_x  =  S_y  =  S_h y S_z  =  S_v,

entonces la ecuación anterior queda:

S_h  -  $${\frac{{1}}{{m}}}$$(S_h  =  S_v)  =   0

S_h(1  -  $${\frac{{1}}{{m}}}$$)  =  S_h$${\frac{{(m\ -\ 1)}}{{m}}}$$  =  $${\frac{{S_v}}{{m}}}$$

S_v  =  $${\frac{{S_v}}{{(m\ -\ 1)}}}$$.

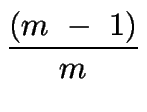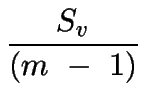De la relación anterior se puede ver que si m  =  2 ($\nu$  =  0, 5), entonces S_h  =  S_v, es decir, el sistema es análogo a un estado hidrostático que desarrollan los líquidos en reposo. Se observa además que para la situación estudiada, el stress causado por gravedad no puede dar origen a un stress horizontal mayor que el stress vertical y por lo tanto, el mínimo valor de m es 2,0 ($\nu$  =  0, 5).

Otros módulos elásticos

El módulo de Young y la razón de Poisson son los parámetros elásticos más fácilmente determinados experimentalmente. Sin embargo, el comportamiento elástico puede relacionarse también con cambios de volumen y distorción angular.

Módulo de compresibilidad (K)

Se utiliza para describir la relación entre el cambio de volumen (dilatación, $\Delta$ e₁  +  e₂  +  e₃) y el stress hidrostático [$\sigma$  =  ($\sigma_{1}^{}$  +  ${\frac{{\sigma_2\ +\ \sigma_3)}}{{3}}}$]:

K  =  $${\frac{{dP}}{{dV}}}$$  =  $${\frac{{\sigma}}{{\Delta}}}$$.

Módulo de cizalle (G)

Relaciona pequeños cizalles angulares ($\psi$) con el stress de cizalle aplicado:

G  =  $${\frac{{\tau}}{{\psi}}}$$.

G y K no son fácilmente determinados por mediciones directas, pero puede ser demostrado que se relacionan con E y m:

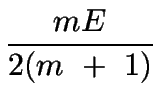G  =  $${\frac{{mE}}{{2(m\ +\ 1)}}}$$        K  =  $${\frac{{mE}}{{3(m\ -\ 2)}}}$$.

Viscosidad

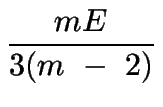Cuando un líquido es puesto en un recipiente de forma irregular, éste adopta la forma del contenedor en un tiempo relativamente corto. Este comportamiento muestra que un líquido perfecto no posee una resistencia inherente al cizalle, de manera que él puede fluir (en algunos lentamente) bajo la acción de un stress de cizalle infinitamente pequeño. Una mayor velocidad del flujo se asocia a un aumento en la magnitud del stress de cizalle (por ejemplo un arrollo).

Para muchos líquidos la relación entre el stress de cizalle ($\tau$) y la tasa del strain de cizalle (${\frac{{d\gamma}}{{dt}}}$) es lineal:

$$\eta$$  =  $${\frac{{\tau}}{{\frac{d\gamma}{dt}}}}$$

donde $\eta$ es una constante del material conocida como el coeficiente de viscosidad.

Los líquidos que tienen una relación lineal son conocidos como líquidos newtonianos y los que no presentan una relación lineal se denominan no newtonianos.

Plasticidad

Mientras la teoría de la viscosidad se relaciona con el comportamiento de un líquido, la teoría de la plasticidad se refiere al comportamiento de un sólido.

La relación entre stress y strain para un cuerpo rígido perfectamente plástico muestra:

1. Cuerpo rígido, plástico.
2. Cuerpo elástico, plástico.
3. Cuerpo elástico, plástico, con strain hardening.

Figura 10.1: Cuerpo rígido plástico, cuerpo elástico plástico, cuerpo elástico plástico con strain hardening.

Bajo pequeños stresses el cuerpo no presenta ninguna distorción. El flujo plástico comienza sólo cuando la carga alcanza la resistencia crítica. Teóricamente es posible desarrollar una deformación plástica ilimitada bajo este stress crítico.

Sin embargo, uno no debería esperar un comportamiento perfectamente plástico de una sustancia natural, ni siquiera a bajos niveles de stress. A bajos niveles de stress el comportamiento más probable es elástico. El modelo mencionado representa un cuerpo elástico-plástico (b). Comúnmente se encuentra que una vez que ha sido alcanzado el esfuerzo mínimo de deformación permanente, (yield point), hay que incrementar ligeramente el stress para que continúe la deformación plástica. Esto se denomina strain-hardening (c).

Una analogía mecánica del flujo plástico es la resistencia friccional de un bloque que yace sobre un plano. Una vez que el deslizamiento ha comenzado, la fuerza aplicada no puede sobrepasar la resistencia a la fricción del material, excepto para acelerarlo.

Investigación experimental de flujo dúctil

Una manera de ensayar materiales como rocas, metales, cerámica, etc., es someter, a una carga constante, un especimen de forma regular, usualmente cilíndrica y registrar el cambio de strain de la muestra con el paso del tiempo. Este tipo de experimento se conoce como ensayo o test de creep.

Inicialmente, tan pronto como el especimen es sujeto a una carga, exhibe un strain elástico AA'. Este es seguido por un período caracterizado por una disminución de la tasa de strain A'B, conocido como "creep primario''. Esta fase se denomina también creep tiempo-elástico. Si en un tiempo t₁ la carga es removida del especimen, habrá una recuperación inicial instantánea (BB') seguida por una recuperación (B'C) denominada tiempo elástica, la cual es completada cuando el strain vuelve a 0. Si el especimen es descargado en un tiempo t₂, exhibirá una recuperación instantánea y una recuperación tiempo-elástica (DD') (tiempo de relajación elástica). El strain, sin embargo, no es totalmente recuperado y existe en strain residual, no recuperable y permanente. Si el especimen no es descargado en t₂, se observa que la fase de creep secundario pasa a un estado de aceleración e creep terciario, el cual eventualmente lleva a la ruptura del material.