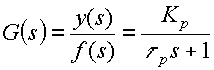
Si un sistema de primer orden

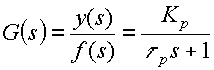
es excitado por una entrada sinusoidal de amplitud A y de frecuencia w ,

entonces, la entrada al proceso será:

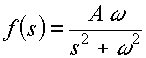
de modo que la respuesta del proceso será:

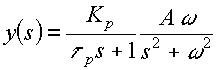
que, al destransformar (vía fracciones parciales, etc.) da una respuesta final (i.e. a tiempo infinito) de carácter oscilatorio también,

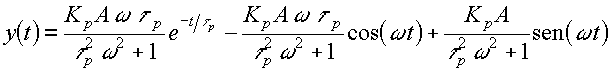
porque el término exponencial se extingue a t extenso; es decir, la respuesta del nuevo estado estacionario será:

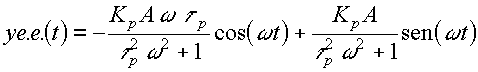
o, que es lo mismo por identidades trigonométricas:

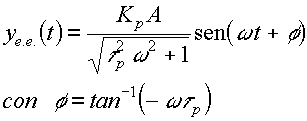
Se puede concluir, al menos, que:

1. El nuevo estado estacionario (de un primer orden con entrada sinusoidal) es una respuesta escilante, de la misma frecuencia que la entrada.
2. La amplitud de la respuesta es una función tanto de la amplitud de la entrada como de la frecuencia (de allí que se suele hablar de la Razón de Amplitudes):




3. La respuesta se retrasa respecto de la entrada en un ángulo de fase f , que depende de la frecuencia de entrada.

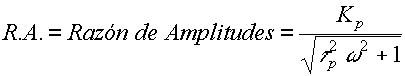
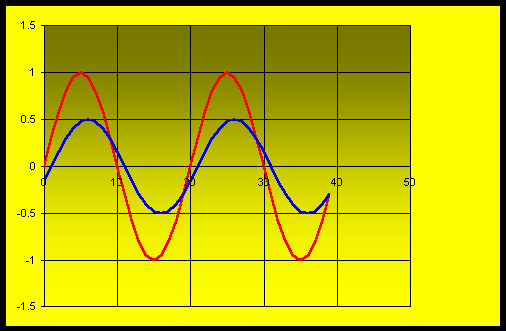
Si la línea roja fuese la entrada y la azul la respuesta, entonces la R.A. sería del orden de 0,5. ¿Cuánto será el ángulo de fase? ¿En qué unidades?

Si se considera un número complejo cualquiera, en la forma

Se dice que la magnitud "a" es su parte real y la magnitud "b" su parte imaginaria; mientras tanto, "j" representa un eje ortogonal y su magnitud es la raíz cuadrada de "-1"

Entonces, como notación, se puede usar que a=Re(W) y que b=Im(W)

El "Módulo" (o valor absoluto) del número complejo "W" se asocia a la magnitud de un vector tendido entre dos ejes ortogonales (norma Euclidiana):

mientras que su "ángulo de fase" (o su argumento), representado por ang(W) está definido como el ángulo que tendería el vector:

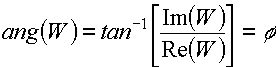
Además, será útil recordar las conocidas relaciones:

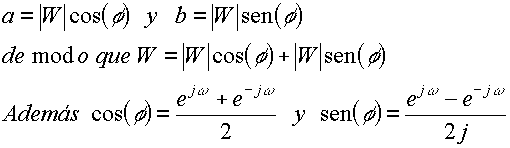
Similarmente, es fácil demostrar que si Z=a-jb y W=a+jb entonces sus módulos son iguales y su argumentos son inversos aditivos (arg(Z) = - arg(W)).

Un método tradicional para encontrar la magnitud y fase de un función de transferencia consiste en evaluarla cuando la variable compleja "s" vale "jw". Por ejemplo, dada la función de transferencia de primer orden que se está analizando:

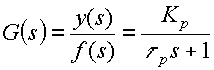
su evaluación cuando "s= jw" y una pequeña manipulación resulta en:

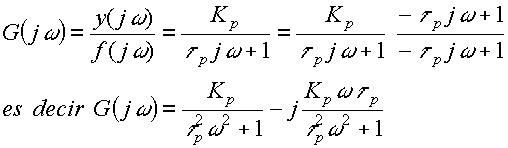
que permite deducir, sin mayor manipulación posterior, que:

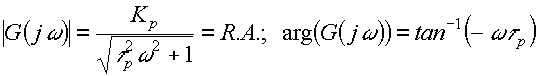
De donde se deduce una regla práctica común para un proceso de primer orden, excitado por una entrada oscilante

La relación de amplitudes y el retardo de fase de la respuesta a tiempo infinito de un proceso corresponden al módulo y argumento de su función de transferencia evaluada en s=jw .

Este resultado será útil para resolver cálculos de R.A. y de arg() en forma simplificada... pero tiene más implicaciones aún.

Cualquier sistema lineal generará, siempre, una función de transferencia consistente de la razón de dos polinomios (Q(s) en el numerador y P(s) en el denominador) donde el denominador (P(s)) es de más alto orden que el numerador (Q(s)):

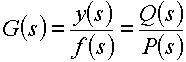
Si esta función de transferencia es sometida a una entrada f(t) sinusoidal, se puede demostrar (el lector está capacitado para realizar la demostración) que:

1. La respuesta a tiempo infinito es una sinusoide, a la misma frecuencia
2. La Razón de Amplitudes es función de la frecuencia y queda determinada por el módulo de la función de transferencia evaluada en s=jw
3. La salida sinusoidal se retrasa en un ángulo cuyo valor queda determinado por el argumento de la función de transferencia evaluada en s=jw

Por ejemplo:

Un proceso capacitivo puro, cuya función de transferencia es G(s)=K_p/s, al ser evaluada en s=jwpermite deducir que:

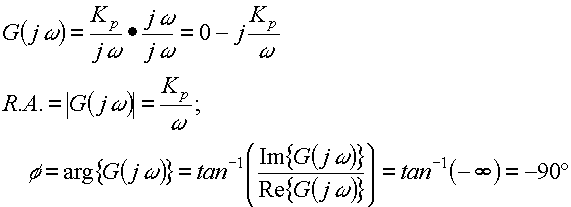
Es decir, la respuesta de un proceso capacitivo puro a una entrada sinusoidal es una oscilación de la misma frecuencia retardada en 90º de arco.

Es recomendable que los estudiantes ensayen en el sistema de estanque con bomba de descarga de Control Station una oscilación centrada en 20, de amplitud 2 y de períodos de 100 y 200 segundos para ratificar los resultados anteriores.

Como otro ejemplo, será útil calcular la R.A. y arg() de un sistema compuesto por N capacidades conectadas en serie no interactuante, ya que genera una función de transferencia de orden N pero cuya respuesta a un escalón es siempre una sigmoídea.