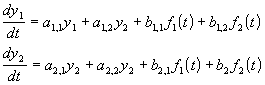
Son diagramas que permiten sintetizar las relaciones entre las entradas y salidas de un proceso, mediante su modelo matemático. El modelo debe ser lineal y estar expresado como modelo entrada/salida para construir la Función de Transferencia del proceso (que es la división de la transformada de Laplace de la respuesta dividida por la transformada de la entrada.
Los procesos pueden tener varias entradas y varias salidas. Se podría hablar de un vector que relaciona la salida (o respuesta) de un sistema con sus diversas entradas (o excitaciones).
Similarmente, se debiera poder analizar un sistema de varias excitaciones y varias respuestas. Por ejemplo:
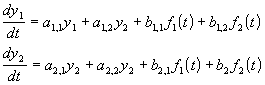
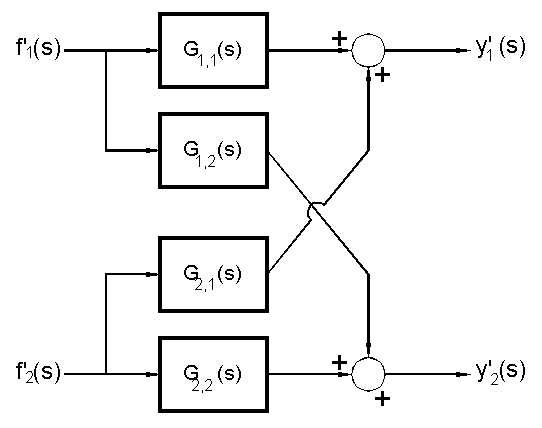
generaría una matriz de funciones de transferencia (existen 4 funciones de transferencia que relacionan dos entradas [o excitaciones] f con dos salidas [o respuestas] y) de manera que el vector de salidas se obtiene como el producto de una matriz G por el vector de excitaciones.
|
RPA con enfriamiento
|
A
à B, exotérmica; Frío a tasa Constante; NOTA: Multiestable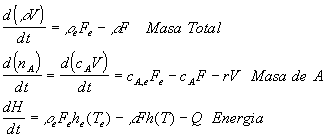
Donde rho es la densidad, n el número de moles, r la cinética y Q el balance de calores.
Este modelo NO ESTÁ en la forma adecuada para su uso en análisis dinámico o control del proceso. Se debe establecer el MODELO ENTRADA/SALIDA, de modo que lo primero será identificar las variables de estado apropiadas.
Por ejemplo, la ecuación de masa se puede simplificar si es aceptable la hipótesis de densidad constante, porque en tal caso, sólo se necesita V para caracterizar completamente la masa total. (dV/dt=Fe-F).
Luego, para la masa de A, se puede elegir como variables de estado el Volumen de reacción (V) y la concentración de salida de A. La cinética r estará dada por un coeficiente base y una exponencial de la temepratura de reacción :
![]()
En fin, para la energía del sistema, usando las hipótesis habituales (que deben ser verificadas de a una en una) en términos de entalpía de A y de B, además de aproximaciones para las entalpías molares parciales y que el cambio de entalpía es igual al cambio de energía, manipulando y simplificando algebraicamente, se puede optar por usar T como variable de estado (esto podría ser obvio desde el inicio).
Observe que ahora, a diferencia de la ecuación anterior, Q representa el calor removido por el servicio de enfriamiento (en lugar del balance de calores):
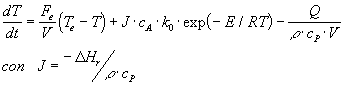
Debiera ser ahora posible identificar las variables, según la nomenclatura estándar (entradaa y salidas):
|
Salidas |
V, cA, T |
|
Entradas |
cA,e, Fe, Te, Q, F |
|
(Perturbaciones |
cA,e, Fe, Te) |
|
(Manipuladas |
Q,F (podrían ser Fe o Te) |
|
Parámetros |
r , cP, (-D Hr), k0, E, R |
El objetivo del modelo es entregar una relación (matemática y realista) de las variables de salida: V(t), cA(t) y T(t). Según se declaró más arriba, el volumen de reacción se podría considerar constante (en cuyo caso V es un parámetro del modelo) o sufrir pequeñas pertubaciones (en cuyo caso, V será una perturbación).
Aún si se asegura constancia del volumen de reacción, quedan dos ecuaciones. Estas ecuaciones tienen términos no lineales, que son habituales en reacciones químicas.
![]()
![]()
Se debe linealizar el término "exp", en torno a un punto general, (cA,0., T0.). Se observará que la no linealidad corresponde tanto al término exponencial en T (variable de salida) como al producto de la variable composición CA por el término cinético en T. Es decir, se debe desarrollar una aproximación lineal en ambas variables. Si la aproximación lineal corresponde a una serie de Taylor:
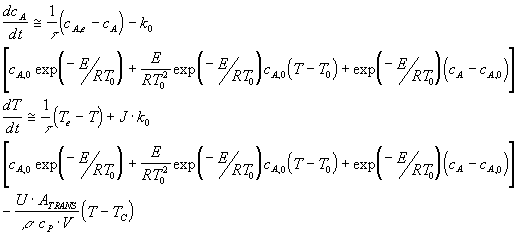
Se obtuvo una aproximación lineal que puede ser transformada por Laplace para facilitar su manipulación. Sin embrago, es útil expresar las variables como DESVIACION EN TORNO A UN ESTADO ESTACIONARIO (CA,e Te), que arroja
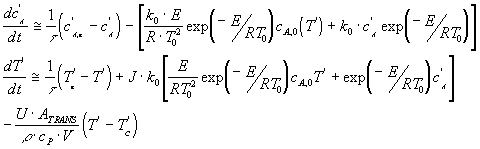
que es ya una expresión que puede arrojar un modelo E/S apropiado.
El modelo será:
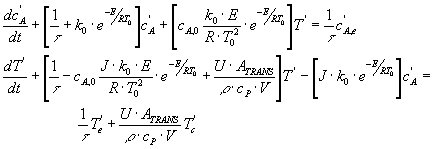
Donde al transformar , obviamente, aparecen 6 funciones de transferencia que ligan 2 SALIDAS con las 3 ENTRADAS.
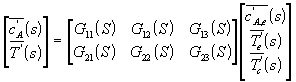
que pueden ser expresadas en diagramas de bloques según:
Todas las funciones de transferencia comparten el mismo polinomio en el divisor (que el alumno debiera encontrarlo), el que recibe el nombre de Ecuación Característica, cuando se escribe el polinomio del denominador igual a cero (
los términos aij provienen del sistema de ecuaciónes diferenciales ordinarias anterior):![]()
Por definición de la
FUNCIÓN DE TRANSFERENCIA, G(s), corresponde a la razón de la transformada de Laplace de la salida respecto de la transformada de Laplace de la entrada: G(s)=Y(s)/F(s).En general, la función de transferencia corresponderá a la razón de dos polinomios, numerador Q(s) y denominador P(s):
![]()
(exceptuando las Funciones de Transferencia de modelos con retardo, que introducen un término exponencial en s)
Para sistemas Físicamente factibles, orden(Q)<orden(P)
Los ceros (o raíces) del polinomio en el denominador, P(s), se denominan POLOS de G(s), pero también
POLOS DEL SISTEMA modelado.Por ejemplo, los POLOS del RPA de A
à B exotérmico, a V cte son: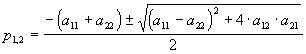
![]()
y es también el caso que la Transformada de Laplace de muchas funciones de entrada es una razón de polinomios
![]()
de modo que la respuesta del sistema es otra razón de polinomios:
![]()
La inversión (Laplace) de la respuesta requiere conocer las fracciones parciales, para lo cual sería útil conocer las raíces de P(s) y de q(s). Estas raíces serán los polos de y(s). La respuesta en el tiempo está unívocamente determinada por los polos de y(s).
Conocida la localización de los polos de un sistema, se conocen las características cualitativas de la respuesta del sistema para cualquier entrada en particular.
Si pi es una raíz de P(s) (i recorre hasta el orden de P(s), naturalmente)
![]()
(además * = Conjugación) entonces, la expansión en fracciones parciales será:
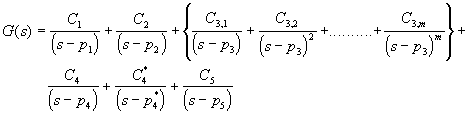
En esta expresión es posible distinguir distintos comportamiento de la función G(s) según la localización de cada polo en el plano complejo. El comportamiento cualitativo se relaciona tanto con la posición (real puro, imaginario puro, cuadrante que ocupa, etc.) como con la magnitud.
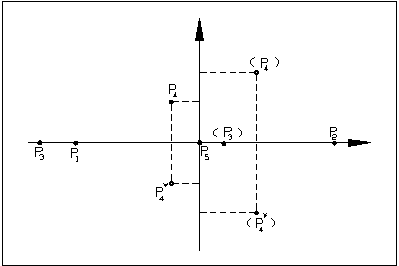
I.-
p1 y p2 son dos raíces reales distintas. Al invertir su transformación generan términos exponenciales del tipo![]()
Como p1<0, la primera solución decae hasta cero conforme t
ॠ. Pero, dado que p20, la segunda solución crece eternamente.Polos en el eje real negativo
è soluciones que decaen en el tiempo.Polos en el eje real positivo
è soluciones que crecen en el tiempo.II.-
p3 es un polo múltiple de orden m que genera soluciones del tipo![]()
Obviamente, el término en el paréntesis crece hasta infinito con el tiempo. El término exponencial, en cambio, depende del valor del polo p3:
Si p30, exponencial tiende a infinito con el tiempo
Si p3<0, exponencial tiende a cero con el tiempo
Si p3=0, exponencial vale siempre 1
Un polo real múltiple positivo o cero genera una tendencia a infinito.
Un polo real múltiple negativo genera una tendencia a cero.
III.-
p4 y p4* es un polo complejo conjugado. Naturalmente, siempre que un polo sea complejo, también será polo su conjugado.Tomando p4=
a +jb, entonces p4*=a -jbque generan soluciones del tipo eatseno(b t+j ). El término seno es simplemente oscilatorio, mientras que el comportamiento del término exponencial depende de a.Sia 0 la solución tiende a infinito, de forma oscilatoria
Sia <0 la solución tiende a cero, de forma oscilatoria
Sia 0 la solución oscila permanentemente.
IV.- p5 es un polo en el origen. El sistema tiene un solución constante
NOTAS:
1.- Este análisis es siempre válido, e independiente de f(t)
2.- Polos a la derecha del eje imaginario genera términos que tienden a infinito en el tiempo (INESTABLES).
Respuestas Características de los Sistemas
Dinámica de Primer orden
, Utilizando variables desviación, y(t)=0, f(t)=0 en t=0.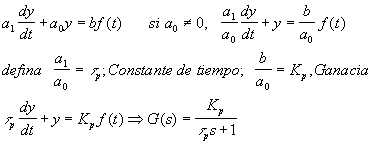
Por otra parte, si a0=0,
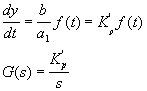
conocido como proceso "puramente capacitivo". El análisis de la respuesta dinámica de un sistema puramente capacitivo consiste en determinar como cambia y(t) con f(t). Por ejemplo, frente a un cambio escalón (cuya transformada es 1/s):
![]()
Es decir, un cambio escalón produce un incremento permanente en el tiempo. Recibe, por eso, el nombre de "integrador puro". Se observa que un sistema capacitivo puro produciría serios problemas de control, comportándose como un sistema no autoregulado, que requiere un controlador. (Estanque con bomba de desplazamiento positivo en la salida).
Similarmente, la respuesta dinámica de un sistema de primer orden de respuesta exponencial, o de retardo, se puede analizar frente a un cambio escalón (si bien es posible y deseable utilizar otras funciones de entrada, pero un primer orden es suficientemente simple).
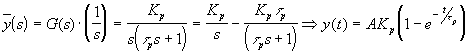
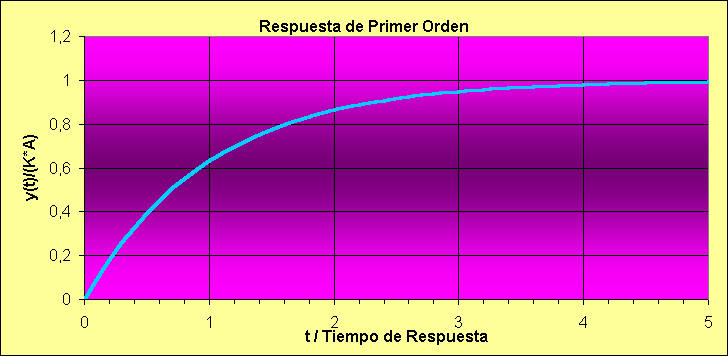
Obviamente, la respuesta a tiempo infinito es la misma amplitud del escalón, es decir, finita, de allí que se llame autoregulado, pues llega a un nuevo estado estacionario aún cuando no se tome acción alguna.
La pendiente del gráfico adimensional en tiempo cero es 1,0 (es decir, la curva trazada desde 0,0 siguiendo la pendiente llegaría a 1,1).
Se puede observar que SIEMPRE la respuesta será de un 63,2% en
tp unidades de tiempo, 86,5% en 2tp, 95% en 3tp, 98% en 4tp, etc.Habitualmente se trabaja con parámetros constantes. Se debe observar, sin embargo, que los parámetros SON una FUNCIÓN de la operación física modelada de modo que podrían no ser constantes.
Por ejemplo, en el estanque de altura variable con salida regulada por pérdida de carga,
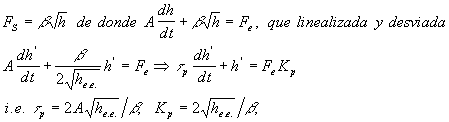
pero he.e. depende del tiempo!!!
Segundo Orden
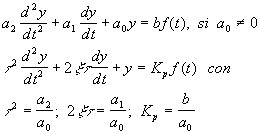
Puesto en la forma canónica,
t es el período natural de oscilación; x es el coeficiente de amortiguación y Kp es la ganancia de estado estacionario.Si se utilizan variables desviación (para que los valores iniciales sean cero, es decir y(t)=0, dy/dt=0 para t=0) entonces
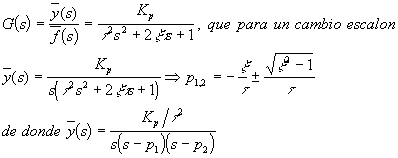
En esta expresión no se puede tomar transformada inversa sin conocer el término dentro de la raíz. Se pueden distinguir tres casos, si
![]() x 1, dos polos reales distintos
x 1, dos polos reales distintos
![]() x =1, polo doble real
x =1, polo doble real
![]() x <1, dos polos complejos conjugados
x <1, dos polos complejos conjugados
Respuesta Sobreamortiguda,
x 1en caso que existan dos polos reales, mediante expansión en fracciones parciales y transformada inversa para un cambio escalón unitario:
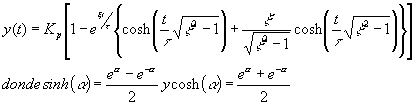
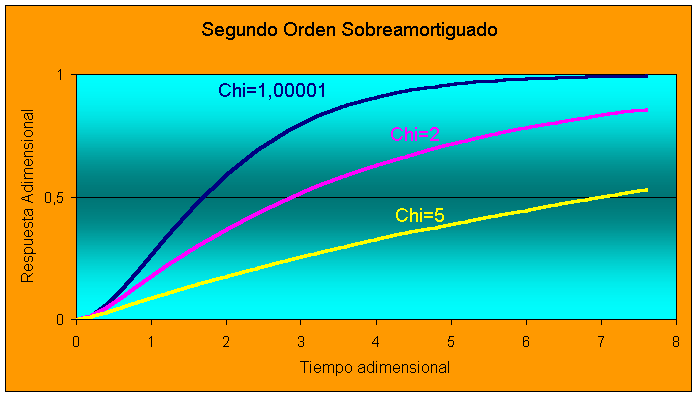
Resulta aparente que la forma de la respuesta se asemeja a una de primer orden pero con un cierto retardo.
El eje y del gráfico anterior se obtiene tomado la respuesta dividida por la magnitud del escalón (si no fuese unitario) y por la ganancia del proceso. El eje tiempo se obtiene dividiendo el tiempo real por el tiempo de respuesta del proceso.
Respuesta críticamente amortiguada,
x =1En este caso, la transformada inversa arroja de la respuesta (y(s)) para un cambio escalón unitario arroja la solución para el dominio del tiempo:
![]()
cuya representación gráfica es prácticamente idéntica a la indicada en la gráfica anterior para
x prácticamente 1. De hecho, es una buena idea que el estudiante verifique que la solución para x mayor que 1 tiende a la solución dada para x =1, al tomar límites.El estudiante observará que la respuesta críticamente amortiguada es
la más rápida respuesta posible de un sistema de segundo orden que no oscile.Respuesta Subamortiguada,x <1
En este caso, los polos de la función de transferencia son un número complejo y su conjugado. La transformada inversa arroja:
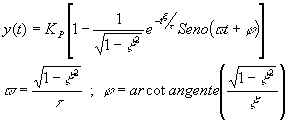
que da origen a soluciones oscilatorias, con frecuencia y ángulo de fase determinados según se indicó en la ecuación.
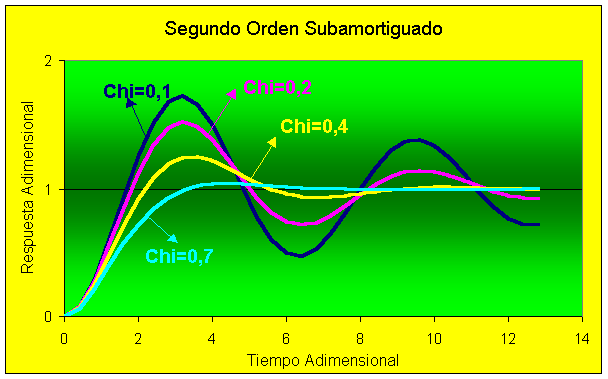
En la gráfica se observa el comportamiento general, según cambia el coeficiente de amortiguamiento (x ). El estudiante podrá observar las siguientes reglas generales:
Es muy habitual encontrar este tipo de respuesta en procesos químicos controlados... no porque las unidades de proceso respondan de este modo sino que, más bien, porque los controladores los ajustamos para que respondan rápido.
En la práctica de procesos no se suele describir el comportamiento en términos de la ganancia, el tiempo de respuesta o el coeficiente de amortiguación; estos parámetros pertenecen al ámbito de los ingenieros dedicados al control de procesos y no a su operación. Así, es útil describir el comportamiento subamortiguado en términos más empíricos y gráficos.
Al igual que para sistemas de primer orden, la respuesta del sistema a un cambio en sus entradas (entrada o perturbación) después de un largo tiempo (infinito, en realidad) llega a un nuevo estado estacionario. En este caso, la tendencia hacia el valor final podría corresponder a una oscilación amortiguada o a una tendencia exponencial. En cualquiera de estos casos, la ganancia estacionaria del proceso estará dada, como antes, por la razón entre la magnitud del escalón aplicado y la magnitud del cambio observado en la respuesta:
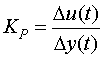
donde se ha denotado por "u(t)" la entrada y por "y(t)" la respuesta.
Los sistemas de segundo orden en todo caso, presentan características nuevas, respecto de los de primer orden. En perticular, pueden oscilar (o no) amortiguadamente. Los sistemas que convergen exponencialmente a un nuevo estado estacionario se denominarán sistemas sobre amortiguados. El caso más típico resulta de sistemas en que el segundo (o mayor) orden se por la interconexión en serie de dos sistemas de primer orden. Habitualmente es posible (y útil) aproximar la respuesta sobre amortiguada de segundo orden a un modelo de primer orden.
Cuando la respuesta de segundo orden corresponde a sistemas críticamente amortiguados (x =1) se obtiene la más rápida respuesta no oscilatoria del sistema. En este caso, según se puede observar en la gráfica de respuestas de segundo orden, la llegada al valor final es más rápida que para los sistemas sobre amortiguados.
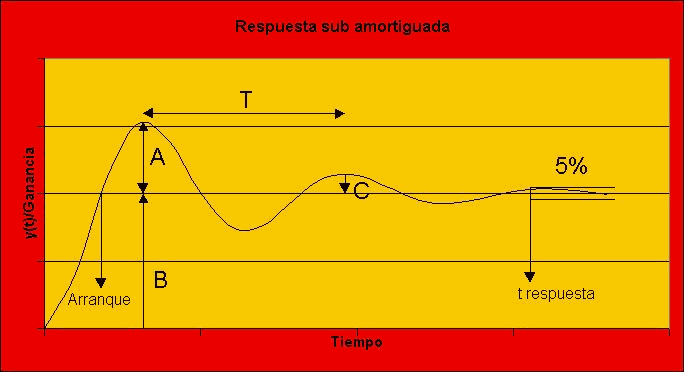
Cundo la respuesta es oscilatoria (x <1), se dice que el sistema está sub amortiguado. La amplitud de la oscilación depende de cuan menor que 1 sea el coeficiente de amortiguación. En este caso es posible caracterizar la oscilación en términos de su evidencia visual, en lugar de tener que determinar por ajuste de funciones, los parámetros característicos de este segundo orden. Se habla, entonces, de:
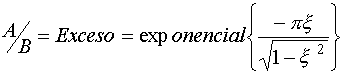

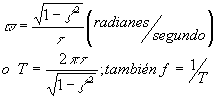
Todos estos conceptos se han capturado en la gráfica de características de las respuestas sub amortiguadas.
Controladores: P, I, D, PI, PID
Control Proporcional
: Gc = KcControl Integral puro
: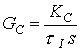
Control DERIVATIVO puro
:En este caso, la acción de control, relativa al error, en el campo transformado será: ![]() .
.
Nuevamente, suponiendo que el sistema de medición y de actuación final son ideales (GM=1; GF=1), la respuesta del bucle cerrado para un proceso de primer orden será:
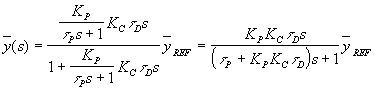
![]()
entonces:
Naturalmente, si se considera un proceso de segundo orden que está subamortiguado, la acción de un control D podría ser útil para sobreamortiguarlo. La capacidad de incrementar la amortiguación y decrementar la rapidez de la respuesta se utiliza para generar sistemas más robustos que los existentes sin control.
Acción de Controladores Compuestos
Se utilizan controladores P, PI y PID pero no se utilizan controles I ni D ni PD ni ID.
Acción PI:
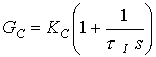
Acción PID:
En síntesis, las características dinámicas son las mismas que para PI.
Existen, sin embargo, beneficios:
PI rápido significa KC grande... ¡pero hay riesgo de inestabilidades porque crece el sobre paso! Si hay acción derivativa, por otra parte, el sobre paso queda casi constante al incrementar KC (dentro de límites razonables), es decir, se acelera la respuesta pero no se incrementa la amplitud de oscilación.
|
Estos bucles de control presentan las características dinámicas anotadas y se debe enfatizar que:La presencia de: |
|
Sensores |
|
Actuadores |
|
Controladores |
|
¡cambia las características dinámicas respecto del proceso sin control! |
Hemos visto que: para un proceso primer orden (i.e. NO Oscilatorio) con un controlador PI puede adquirir características oscilatorias.
Tb., un proceso de segundo orden, oscilatorio pero estable, puede inestabilizarse con un control PI.
Será importante entender la estabilidad de procesos controlados antes de poder diseñar controladores concretos.
Análisis de estabilidad de sistemas realimentados
Estable: Sistema BIBO (bounded input, bounded output):
Sistema que, frente a una excitación acotada produce una respuesta acotada. La excitación puede ser un cambio de referencia o una perturbación. El sistema no debe "dispararse" (es decir, no debe tender a infinito sino que mantenerse acotado).
Acotada: Variable que se mantiene dentro de límites (escalón unitario, sinusoide, diente de sierra, pero NO una Rampa). No-Acotado significa, simplemente, que es muy grande porque en ingeniería real no existe infinito (los tanques se rebalsan, las bombas tienen un caudal máximo, los hornos se funden, etc.)
E.g. inestable: Reactor Agitado con reacción exotérmica y remoción de calor a tasa fija.
Sabemos que si la función de transferencia de un modelo tiene polos en el semiplano complejo derecho (parte real positiva) genera soluciones exponencial de exponente positivo por el tiempo, que tiende a infinito. Así, el modelo es inestable.
La localización de polos nos entrega sólo un primer criterio de análisis de estabilidad.
Si una función de transferencia tiene algún polo con parte real 0, el modelo es inestable.
ESTABILIZACIÓN con control P
Dado un proceso de respuesta ![]()
que es claramente inestable, introduzca un controlador de realimentación negativa de tipo P (con sensor y actuador ideales, i.e. GM=GF=1) y obtendrá la respuesta de bucle cerrado:
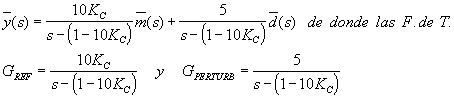
tienen un polo común NEGATIVO si es que KC0,1
Es decir, el control P estabiliza sistemas inestables, si la ganacia del controlador se elige adecuadamente.
DES-ESTABILIZACIÓN con control PI
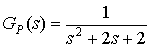
es un segundo orden con dos polos complejos de parte real negativa, es decir, oscilatorio pero estable. P1,2= -1
± j.Introduzca un control PI de realimentación negativa, con GM=GF=1 para obtener la respuesta dinámica a cambios en la referencia según:
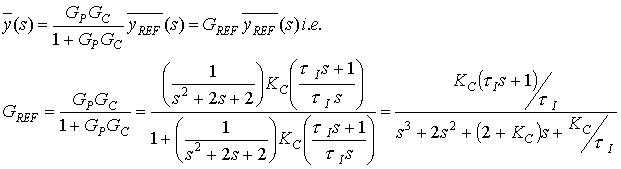
La Ecuación Característica es:
s3 + 2·s2 + (2 + KC)·s + KC/tILuego, como el controlador PI tiene
dos parámetros que se deben elegir y dado que los polos dependen de KC y de tI el comportamiento dinámico será una función de los dos valores elegidos. Elija, por ejemplo, KC=100 y tI=0,1 para poder encontrar los polos des3+2s2+(2+100)s+100/0,1
que resultan ser:
p1=-7,185
p2,3=2,59
± 11,5jde modo que existen 2 polos con parte
real 0.Es decir, el proceso sin control (el así llamado "bucle abierto") es estable mientras que el sistema controlado ("bucle cerrado") PI resulta inestable (con los parámetros seleccionados para el controlador).
Para generalizar esta metodología de análisis de estabilidad, recuerde que la estabilidad, desde el punto de vista de la localización de polos, se analiza mediante la Ecuación Característica que hemos visto que es siempre la misma, tanto para el problema servo como para el problema de regulación. Además, la ecuación característica es siempre (para bucles cerrados de realimentación negativa):
1+GPGFGCGM=a0sn+a1sn-1+...+an-1s+an
que resultará en un polinomio en s de grado "n". Existe, naturalmente, la posibilidad de que "n" sea un número tan grande como para que el cálculo de los polos de la función de transferencia (las raíces de la ecuación característica) sea excesivamente tedioso.
El cálculo de raíces, por otra parte, sólo tiene por objetivo indagar sobre la respuesta dinámica, es decir, bastaría saber si es que existen polos inestables (parte real positiva) y conocer sólo el valor de ellos.
Para el análisis de estabilidad no es estrictamente necesario conocer la localización de cada polo... basta saber si algún polo tiene parte real negativa.
El método (o criterio) de Routh y Hurtwotz permite obtener tal conocimiento.
En primer lugar, el polinomio se escribe de modo que a0 sea positivo.
Luego se aplican los ensayos de polos con parte real positiva.
Si CUALQUIERA de los coeficientes ai (i=1,2, ,,,, n) es NEGATIVO
Þ existe al menos un polo con parte real positiva y el sistema es inestable.Dado que todos los ai 0 (i=0,1, ,,,, n) el primer ensayo resulta inconcluyente.
Se construye la Matriz de Routh, de n+1 filas:

donde
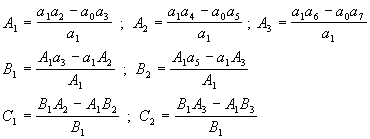
El examen de la primera columna, compuesta de n+1 elementos, arroja la información necesaria final:
Si cualquier número de la primera columna fuese negativo, existe al menos un polo cuya parte real es positiva (sistema inestable)
El número de cambios de signo en los números de la primer columna es igual al número de polos en el semiplano derecho.
ANÁLISIS DE LA LOCALIZACIÓN DE POLOS
La elección de los parámetros del controlador incide sobre la estabilidad del sistema controlado (de bucle cerrado). En el caso anteriormente analizado:
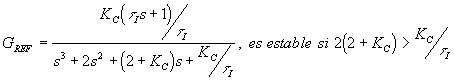
Si se opta por
tI=0,1 el sistema será estable si 0<KC<0,5 (i.e. se obtiene un RANGO estable para la ganancia).El análisis de la localización de polos permite definir los rangos de estabilidad del sistema, mediante un gráfico de las raíces del polinomio característico en función de los valores de la ganancia del controlador, desde cero hasta infinito.
e.g. DOS CAPACIDADES EN SERIE, con sensor y actuador ideales, con controlador P de ganancia KC
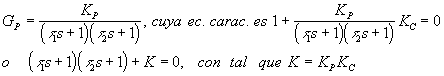
El análisis de localización de raíces se puede realizar para K, ya que es sólo un corrimiento proporcional respecto de KC.
1.- Si la ganancia fuese nula (KC=0, K=0), las raíces corresponden a los polos del proceso (i.e. -1/
t1 y -1/t2)2.- Cuando K crece desde cero, las raíces son:
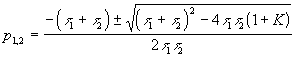
que serán dos reales negativos distintos en tanto el término en la raíz sea positivo, es decir, mientras
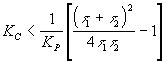
3.- Cuando se cumple exactamente la igualdad, habrá dos raices reales iguales p1=p2=-(
t1+t2)/(2t1t 2).Y, finalmente,
4.- cuando KC excede el límite, se observarán dos polos complejos conjugados
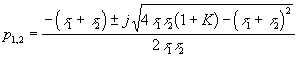
donde se observa que la parte real es negativa e INDEPENDIENTE de la elección de la ganancia del controlador (y del proceso) mientras que la parte imaginaria tiende a infinito con KC.
CONSTRUCCION DEL DIAGRAMA DE LOCALIZACION DE POLOS
1.- El diagrama comienza en KC=0, es decir en los puntos (-1/
t1, 0) y (-1/t2,0) y2.- se mantiene en el eje real, convergiendo a un punto intermedio, mientras KC cumpla la desigualdad.
3.- En el punto crítico, el gráfico contiene dos rectas que llevan a infinito (positivo y negativo) la parte imaginaria, mientras la parte real se mantiene constante.
CONCLUSIÓN: dado que todo el diagrama de localización de polos está en el semiplano izquierdo, el sistema en bucle cerrado es estable.
Se observa que el método arroja, además, información sobre el comportamiento dinámico del sistema en función de la ganancia del controlador.
Por ende, se podría usar este método para diseñar controladores.
Para sistemas de alto orden se usan programas para obtener los ceros de la ecuación característica pero el método es el mismo.
REACTOR CON CONTROL P
En un reactor se mezclan A y R. las reacciones serán
A+R
à B;El caudal de salida será F y se manipula (proporcionalmente) el caudal de A que será "m", de modo que el caudal de R será F-m. La respuesta de interés será la concentración de C (es decir, se mide C para manipular m). Según Douglas, la FT del proceso es:
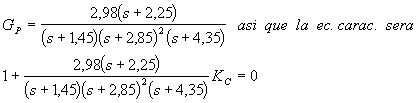
porque se supuso actuador y sensor ideales.
Cuando KC=0, los polos son simples de determinar.
Pero, cuando KC adquiere diversos valores se necesita un método iterativo de determinación de ceros.
Falta aquí el Diagrama Localización ceros en campo complejo y tabla valores de polos y ganancia Kc
Se observa que el sistema es estable para ganancias hasta 50. En algún valor entre 50 y 100, el gráfico cruza hacia el semiplano derecho y el sistema en bucle cerrado será inestable.
Además, para cualquier valor de KC0, pero menor que el valor crítico, la respuesta del sistema será oscilatoria sobre amortiguada (oscilación de amplitud decreciente).
Finalmente, para ganancias mayores que la crítica, la inestabilidad corresponde a polos complejos conjugados de modo que la desestabilización será una oscilación de amplitud creciente.
Este método (localización de polos o de raíces) podría servir para el diseño de controladores, porque el diseño requiere saber:
1.- ¿Que tipo de controlador se debe usar para una aplicación particular?
2.- ¿Cómo seleccionamos los valores de los parámetros del controlador?
3.- ¿Qué criterios de eficiencia debieran usarse para sintonizar los parámetros del controlador?
¿Cuándo se obtienen sistemas de alto orden?
Al conectar sistemas de primer orden en serie se obtienen sistemas de mayor orden. Por ejemplo, dos tanques (capacidades) se pueden conectar en serie no interactuante (uno descarga al otro) o interactuante (por vasos comunicantes). Las Capacidades No Interactuantes:
![]()
donde la SALIDA del primero afecta al segundo, pero el primero NO ES afectado por el segundo. Naturalmente, se puede generalizar a "n".
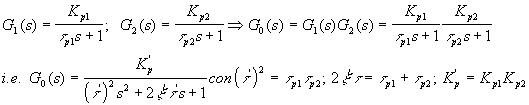
Los polos son dos reales distintos (i.e. p1= -1/
tp1 ; p2= -1/tp2). Claro que ambos tiempos de respuesta pudieran ser iguales (dos polos iguales). En cualquier caso, el sistema es siempre estable.Frente a un cambio escalón unitario, la respuesta será
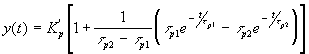
Para "n" capacidades no interactuantes en serie, la ganancia (numerador de la función de transferencia) será el producto de las ganancias estáticas y el denominador estará dado por los polos de cada sistema capacitivo de primer orden i.e. multiplicatoria de (
tis+1)Para capacidades interactuantes (vasos comunicantes) se debe definir la forma de relación entre ambos, por ejemplo mediante una resistencia asociada al flujo entre ellos. Además, la salida del segundo debe tener una forma conocida, por ejemplo asociada a otra resistencia al flujo, pues de otro modo no mantiene el nivel.
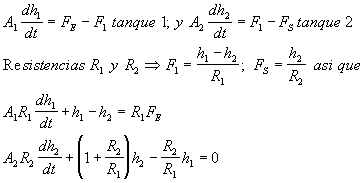
Es decir, se genera un sistema de dos ecuaciones simultáneas de primer orden, en lugar de una ecuación de segundo orden.
Recuerde que los sistemas de alto orden pueden tener (o no) comportamientos inestables, según sea su coeficiente de amortiguación y que este coeficiente es una función de los parámetros físico/químicos del sistema.